センター試験数学II・B【2009年】の難易度、傾向は？

2014/10/19 2016/12/17

2009年に行われたセンター試験IIBに関して、難易度や傾向について情報をまとめていきます。

【評価指標】

１．難易度　A(易)～E(難)

２．パターンレベル
Lv.１(習得していて当たり前)
Lv.２(習得していないと、差をつけられる可能性がある)
Lv.３(習得していなくてもしょうがない)

３．解答するまでの標準的な時間

です。これら３点から、各問題ごとにコメントしていきたいと思います。

センター試験数学Ⅱ・B（２００９年）

０．2009年のセンター試験数IIBの平均点

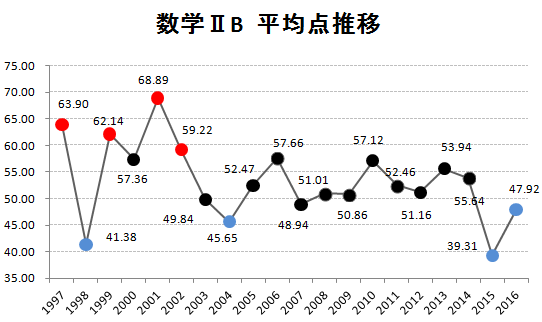
まずは、1997年からの平均点推移を掲載しておきます。赤丸は平均点の高かった年ベスト４、青丸は平均点の低かった年ベスト４です。

（データを元にKATSUYAが作成　グラフの転載可）

今回の2009年は、50.86点となっています。点数から見ると、難しい年のグループに入りそうです。

１．全体評価～慣れないタイプの問題が散見され、やや難

すべての大問において、慣れないタイプの問題が散在し、試験場では動揺しやすいセットであったと考えられ、全体として例年に比べて難。

第１問の前半の指数・対数は、領域内の最大・最小との融合で新タイプ。後半の三角関数は、値から角度の範囲を評価させる問題があった。

第２問の微積は例年並み。軌跡が一部あり。最後の面積はグラフを正確に書かないと領域が把握できない。

第３問は（等差）×（等比）のΣ計算であるが、普段見慣れている過程と異なり、誘導の意図が汲み取れないと後半壊滅の可能性あり。（実は普段の解き方とほぼ同じ！）

第４問のベクトルは正四角錐。座標等は非常に単純でシンプルな図形であるが、文字が多く、かつ図形的意味を用いてうまく計算をしないと混乱する。

■目標解答時間・・・・８０～９０分

数Bを中心に、どの問題も例年より少し時間がかかります。数列、ベクトルは意図を汲み取る時間も取られそうです。

２．各大問の難易度

第１問[1]　(指数・対数　領域と最大・最小　AB　例年並み　新傾向　１０分)

対数式の最大、最小を求める問題です。s、tへの置き換えと範囲は、最初の式に当てはめればすぐに出せます。求めた条件はすべて不等式ですから、最大・最小を求めるには領域図示がいいでしょう。

Principle Piece Ⅱ-53

不等式条件は領域図示　領域との共有点条件

（Principle Piece 数学Ⅱ 図形と式 pp.57～59）

第１問[2]　(三角関数、三角方程式、倍角、角度の評価　AB、やや易、新傾向、１０分)

2010年と同じく、三角方程式を解く問題です。前半は三角関数の性質を利用して角度を求めます。その解を満たす角について評価を行うものです。2つの解を満たす角度の関係は、たすと180°になることを利用し、直前で出した評価を使えば、以下のようにできます。

（※度数法で書きます。）

36°＜θ1<45°
180°ー45°=135°＜θ2<180°－36°=144°

135°÷45°=3<θ2/θ1<144°÷36°=4　
（θ2の最小÷θ1の最大と θ2の最大÷θ1の最小の間）

nは３と４の間なので、最小のnは４であればOK。

第２問(対称点、軌跡、接線、最大・最小、面積、B、例年並み、１８分)

最初は対称点およびその軌跡についてです。軌跡の放物線の式を間違えるとその後全滅なので、少し意地悪な設定になっています。

連動形の軌跡では、移す前の点を（s、t）、移動先をx、yとし、s＝（xの式）、t＝（yの式）　とします。s、tはある曲線上を動くので、その式に代入するとx、yの式になりますね＾＾

Principle Piece Ⅱ-49

連動形は動点を(s、t)、求める点を（x、y）

（Principle Piece 数学Ⅱ 図形と式 pp.48～49）

放物線Dの式が正確に出せれば、接線の方程式はOKですね＾＾

後半です。三角形の面積は、PHを底辺、Pのx座標とRのx座標の差を高さと見れば３次関数として出ますので、微分→増減表で最大値もでます。

最後は面積計算ですが、その下準備にも計算が必要です。H、Rを通る直線の式を出し、Dとの交点を求めます。なお、片方はx＝ー１ですから、ここで検算可能です＾＾

最後の積分計算の計算ミスだけは避けましょう。

第３問 (等比数列とその和、等差×等比数列の和、B、やや難、新傾向、２０分)

前半は等比数列の問題です。まずはb＿nの和までさっさと出したいところです。

b＿nまでの積の方ですが、b＿nの一般項が(1/3)^(2n-1)　であるとしておくと、指数を足し算すればよいと気づけば出すことができますね＾＾

なお、b_１＝1/3、b_1b_2=1/81=1/(3の４乗)　と試せば埋めることができます。よく分からないときは、穴埋めの性質を活かして埋めてしまいましょう。

問題は後半です。c_nは等差×等比型になっており、その和を求める問題です。一般の参考書に記載されている方法であれば、こちらの原則に従います。

Principle Piece B-４

等差×等比　の和は S－(公比)S を計算

（Principle Piece 数学B 数列 pp.19-20）

しかし、本問は非常に誘導がわかりにくく、この方法を採用していることに気づかない可能性があります。

普段なら、U,および1/9U　をずらしながら横に書き並べて計算し、辺々を引き算します。センター試験だと「横に書き並べる」ことができないため、このような表現になっています。

普段の操作は、U-1/9U　の計算を縦に引く際、かぶっているところの引き算は、c_(n+1)-1/9c_nを計算していることになります。これを９倍すると、9c_(n+1)-c_n　となりますね＾＾　

その次の、和の計算（ス、セ、ソ）はさらに意地悪な誘導になっています。Unをうまく使いたいのでしょうが、テクニカルな変形を要求しています。

9C2-C1
9C3－C2
9C4－C3
9C5－C4
・・・・
9Cn－C_n-1
9Cn+1－Cn

を足します。同じ色の部分はトータルで8倍分になりますので、結局和は

－C1+8(C2+C3+・・・Cn)＋9C_n+1

となります。しかし、Unは　C1+C2+C3+・・・Cn　なので、８（・・・）の中にC1を加える代わりに、ー８C1を先頭からさらに引き、題意の式を得ます。

8(C1+C2+C3+・・・Cn)＋9C_n+1－9C1　
＝8Un＋9C_n+1－9C1　

これが２Tnになることを用いて、Unについて解けば答えが出せる、という流れです。最後の計算も形に合わせるのに苦労しますので、ここは投げた人も多いと思います。

点数を稼ぎに行くのであれば、Unの計算は原則通りに行って最後だけ解答するのがベストだったでしょう。

第４問　(空間ベクトル、三角形・四角形の面積、空間上の直線の交点、２点間の距離、B、やや難、２５分)

対称性の高い四角錐を題材とした空間ベクトルで、最初の内積と面積以降は文字のオンパレードであり、数値計算がほとんどいらない代わりに、図形的意味の理解力を問われるタイプの問題で、差が大きくついたでしょう。

最初の内積と面積はいいですね＾＾　なお、ベクトルにおける面積の求積式を覚えていない人を見かけますが、公式です。使っていいものなので、必ず覚えておきましょう。

このあとは、空間上における２直線が交わることを「示そう」という問題。空間上では、２直線は交わるとは限らないため、交わる状況にあることを示す必要があります。

本問の誘導は、A1B1上のある点、かつAE上のある点が一致することを説明するようになっていますが、はっきりいって大げさです。

OA1→＝OA→＋BB1→
ですから、
AA1→＝BB1→

です。ベクトルの最初に習得すべき原則を覚えているでしょうか。

Principle Piece B-23

AB→＝CD→　ならこの4点は平行四辺形

（Principle Piece 数学B ベクトル pp.6）

平面ベクトルの原則ですが、空間でももちろん成り立ちます＾＾

この時点で、A、A1、B、B1は平行四辺形（同一平面上）ですから、A、A1、B、Eも同一平面上です。平面上では２直線は交わるのは当たり前です。相似を使えば、交点E1について、

A1E1：E1B1＝AA1：EB1＝BB1：EB1＝ａ：１－ａ
となります。

これに気づかないと、そのあとにある「同様に考えることにより」のところでは「何をどう同様に考えるのか」よく分からなくなり、詰まる可能性があります。

同じ比に内分することから、平行線と相似比の性質を△ADEに用いて、D1E1：DE＝ａ：１　となります。

相似比から面積比、そしてその差としてB1C1D1E1（台形）を出せばOKですね＾＾

このように考えれば、計算するのは最後だけです。B1D1ですが、どちらも成分をａで表すのがもっとも早いでしょう。

普段センターで出やすい原則が終始姿を現さず、図形的性質とバランスよくいかないと、解きにくい問題だったと思われます。

※「ここはこんな風に考えて出した！」という人は、どんどんコメントください。数学は、他の人の解き方を聞くことで伸びる科目です＾＾