センター試験 数学I・A【2009年】の難易度、傾向は?
2016/12/17
2009年に行われたセンター試験の数学I・Aに関する情報についてまとめていきます。
【評価指標】
1.難易度 A(易)~E(難)
2.パターンレベル
Lv.1(習得していて当たり前)
Lv.2(習得していないと、差をつけられる可能性がある)
Lv.3(習得していなくてもしょうがない)
3.解答するまでの標準的な時間
です。これら3点から、各問題ごとにコメントしていきたいと思います。
センター試験数学Ⅰ・A(2009年)
0.2009年のセンター数I・Aの平均点~
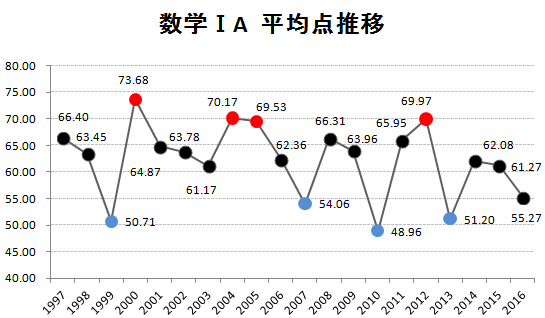
まずは、1997年からの平均点推移を掲載しておきます。赤丸は平均点の高かった年ベスト4、青丸は平均点の低かった年ベスト4です。
(データを元にKATSUYAが作成 グラフの転載可)
今回の2009年は、例年並みの平均点となっています。
1.総評~全分野から典型タイプの出題が多く、例年並み。
最小値の軸分けや円周角の定理、方べきの定理など、センターの傾向から外れない内容のセットで、全体として平年並み。
第1問の因数分解と式の値で、簡単です^^ 後半の必要十分も比較的ラク。
第2問の2次関数は、主軸の「場合分け」に加え、それに加えて最小値の値から定数を決定。最後以外はセンターパターンで、点数は取りやすいか。
第3問もいつもどおりの三角形と外接円、内接四角形などがネタです。参考図も書かれており、半分ぐらいまでは取りやすい。
第4問の確率は例年に比べると少し誘導が少ない。サイコロの目なのだが、最初の誘導で「1、2、3、4」しかないと思いかねないので、ちょっと意地悪。
■目標解答時間・・・・55~65分
まともに解くとこれぐらいかかります。第2問の2次関数の軸分けなどは、記述式で答案としてかけることも大事ですが、センターの時は自分で見ればわかる最低限のことをささっと書いて求めていくようにしましょう。記述モードとセンターモードの両方もモードを確立しましょう。
2.各大問の難易度
第1問[1] (因数分解、式の値、A(例年より易)、5分)
教科書レベルの因数分解および、式の値の計算です。因数分解は、x、yの2次式なので2段階のたすき掛けのパターンですね^^答えの形から見ても、計算をミスしたら発見できるでしょう。ここは落とすとマズイ。
KATSUYAの感想
特につまるところはなし。解答時間1分。
第1問[2] (必要十分・包含関係 AB(例年より易)、6分)
3つの実数の範囲の集合に関する問題です。今回はどの条件も文字が1文字であることもあり、数直線だけで範囲を図示をすればよかったので、ラクです。
KATSUYAの感想
まずはいくつか書き出しで判断。本当にそうなるかどうか、論理的にも考えて終了。解答時間4分。
第2問(頂点、接する、最小値(軸分け)から定数決定、B、例年並み、15分)
2009年の2次関数は主力の軸分けが入っており、標準レベルです。前半の頂点座標、x軸と接するときなどはいつもどおりのパターンです。
後半は最小値の軸分けです。最初は、「軸で最小となるのはいつか」と聞いていますので、軸が定義域内に入るときです。あとはその範囲を外れているときを分けていることになります。
最後は、場合分けした式それぞれにー7/9 を代入して方程式を解きます。出たaが、場合分けした範囲に合っているかどうか、きちんと確かめましょう。
(Principle Piece 数学Ⅰ 2次関数 p.27)
KATSUYAの感想
軸分け+方程式のパターンか。時間を取られるパターンだが、原則に従えば解けるので、落ち着いて処理して終了。解答時間7分。
第3問(内接円、正弦・余弦、円と直線など、20分)
三角比+平面幾何の融合問題です。2009年は普段どおり、外接円と4点型です。∠CABは変形余弦(3辺から角度を出す)で、BD、CDは角の2等分線より成り立つ定理を用いましょう。
正弦、余弦の使い分けは大丈夫ですよね^^
(Principle Piece 数学Ⅰ 三角比 pp.22-23)
後半の等しい角度ですが、角の2等分線なので∠BAD=∠CADで、さらにそれが60°であることも利用すると、∠BEC=180-120=60° で、これも等しくなります。ここから、BCEが正三角形であると見抜ければBEは出ます。DEは△BDEで余弦がいいでしょう。
最後ですが、O'Bはいわゆる外接円の半径Rですので、正弦です。tan∠EBOですが、O'BEが2等辺三角形であることを利用し、これを2等分するのが一番賢いと思われます^^
2010年、2009年とtanを問われていましたが、tanに関する定理はあまりありません。どこかに直角三角形を作りましょう。
KATSUYAの感想
いつもより平面幾何の知識を必要とする部分が少なく、ラクか。回答時間9分。
第4問(場合の数、確率、さいころ、期待値、B、14分)
さいころを繰り返し投げるパターンです。最初の誘導が少し混乱を招きやすく、まるで1~4までの目しか出ないかのように見えます(私だけ??)が、6まであります。
(1)は書き出しが一番いいでしょう。1の目が出て終了するには、和が途中で3にならないとダメです。2の目なら2か3、3の目なら1か2か3、4の目なら0、1、2、3どれでもOKです^^
(2)以上は、5、6の目が出て終了する場合も書き出しておかないといけません。それを今度は回数で分ける作業にはいります。計算で出せないこともありませんが、(1)である程度書き出していること、期待値を出すなら全ての確率が必要であることを踏まえると、書き出したほうが賢明です^^
KATSUYAの感想
計算では出せなさそうか。どうせ期待値出すし、回数も意識しながら全部書き出したほうが早い。(2)以降、5、6の目を無視してケタが合わず、「なんで?^^;」となるが、気付いて終了。回答時間6分。
※「ここはこんな風に考えて出した!」という人は、どんどんコメントください。数学は、他の人の解き方を聞くことで伸びる科目です^^
3.センター試験対策
レベル的には、教科書の章末問題レベルです。そのレベルの問題を、いかに素早く解くかがカギになってきます。
2次で数学がいる人は、特に意識する必要はありません。
2次の対策がそのままセンターの勉強になってます。過去問や模試などで、形式になれることだけしておくといいでしょう。
【必読!! 新課程で受験する皆さんへ】
第3問のような、平面図形と三角比の融合は2015年度センター試験には出ません。みなさんが受ける試験は、数学Ⅰから「三角比」のみ、数学Aから選択で「平面図形」のみとなります。ですので、過去問の第3問で取れなかった人は、悲観するには及びません。 なお、期待値も出ませんが、条件付き確率は出ます。
■関連するPrinciple Piece(2016年度、新課程に合わせた内容に対応しています)■
・Principle Piece 数学Ⅰ 方程式と不等式
(第1問[1] 対応)
・Principle Piece 数学Ⅰ 2次関数
(第2問対応)
・Principle Piece 数学A 論理と集合
(第1問 [2] 対応)
・Principle Piece 数学Ⅰ 三角比
(第3問対応)
・Principle Piece 数学A 集合と場合の数
(第4問対応)
・Principle Piece 数学A 確率
(第4問対応)
・Principle Piece 数学A 整数
(新課程では出題されます!)
・Principle Piece 数学A 平面図形
(第3問対応)
Principle Piece 数学IA 原則のみ
(全問対応)
センター試験対策用の参考書については、こちらのリンクからどうぞ^^