広島大学 理系| 2017年度大学入試数学
2017/10/08
●2017年度大学入試数学評価を書いていきます。今回は広島大学(理系)です。
いつもご覧いただきまして、ありがとうございます。 KATSUYAです^^いよいよ、2次試験シーズンがやってきました。すでにお馴染みになってきたかもしれませんが、やっていきます。
2017年 大学入試数学の評価を書いていきます。
入試シーズン中は、コメントの返信が大幅に遅れることがあります。ご了承ください。
2017年大学入試(国公立)シリーズ。
広島大学(理系)です。
問題の難易度(易A←→E難)と一緒に、典型パターンのレベルを3段階(基本Lv.1←→高度Lv.3)で書いておきます。
また☆は、「解くとしたらこれがいい」というオススメ問題です。
解答までの目標時間を、問題ごとに書きます。
※目標時間=解き方を含め、きちんと完答するまでの標準的な時間です。
したがって、目標時間を全部足すと、試験の制限時間を越えることも、当然ありえます。
同時に、その時間の2倍考えてもまったく手がつかない場合は、ヒントや答えをみるといい、という目安にしてください。
広島大学
(全5問、120分、記述式)
1.全体総評~精緻な計算力が問われる部分が多く難化~
昨年より難化です。昨年は計算量が例年より少なかったですが、今年はリバウンド。例年よりも多めで、制限時間内に解くことが難しい計算量になりました。小問が多く、誘導によって部分点は稼ぎやすいのはいつも通りでした。典型パターンの問題や、思考力を見るものがバランスよく出ている印象です。
試験時間150分に対し、
標準回答時間は160分。今年は少しオーバー気味ですが最後を捨てれば多少はマシ?
2016年:113分
2015年:145分
2.合格ライン
第1問は誘導過剰気味で方針はほぼ決まるので、確実に取りに行きたい。
第2問も誘導は丁寧なので、意味をつなげてなんとか進めたい。最低でも(2)まで。
第3問はキー問題。(2)でしっかり規則をつかめるか。(3)も経験で差がつく。
第4問は広大にしては珍しい出題だが、典型パターン。経験していれば取れるはず。
第5問は易から難へ小問が並ぶ。(2)まで欲しい。そこで規則が分かれば、(3)キー問題。最後以外は解けそう。
1番、2番か4番のどちらかを完答して2完、残りで1完分かき集めれば60%ぐらいとなります。今年はこれでもボーダーに達すると思います。2番と4番が両方できれば、安心ですね^^
3.各問の難易度
第1問・・・【三角関数+数列+極限】漸化式の一般項と極限(B,20分、Lv2)
特殊な漸化式の一般項を求める問題です。(1)で既に予想がつき、(2)でそれを証明するという形です。(3)は三角関数の極限系統なのだな、と誘導のおかげですぐに分かります。
(1)は誘導過剰気味。tan15°は加法定理で出すなりして、一致することを証明しましょう。なお、先に(2)をやっても問題ありません。
(2)は結果を予想して帰納法で証明するというものです。
(拙著シリーズ(白) 数学B 数列 p.50-57)
(3)は三角関数の極限となります。三角関数の極限の基本形の解法は大丈夫ですね。なお、極限の基本形はもちろんですが、それらがみな「x→0」になっていることも大事です。従って、本問は置き換えが必要です。
(拙著シリーズ(白) 数学III 極限 p.39-41)
(拙著シリーズ(白) 数学III 極限 p.40-41)
※KATSUYAの解いた感想
(1)で結果丸分かりに近いけど^^; 先に半分になることを証明しよう。倍角を使って角度を下げて証明し、その結果を(1)、(2)の両方で使う。(3)は三角極限タイプね。1/2^n →t で置き換えればいけるな。解答時間10分。
第2問・・・【図形と式+微分法II】3次関数の最小値、円と4次関数の共有点の個数、距離の最小値(B、30分、Lv.2)
数学IIの融合問題という感じで、最終的には4次関数上の点との距離の最小値を求めるところまで来ます。いきなり出されるとかなり辛いですが、こちらも誘導が丁寧なので、なんとかついていけそうです。
(1)は定数が入っていますが、t≧0、a>0という制限のおかげで、場合分けは不要です。(2)は(1)ができればOK。
(3)は連立すると分かりますが、x=0以外に、(1)で出てきた方程式にそっくり帰着できますので、この解の個数を共有点の個数と結びつけましょう。
(2)を利用すればすぐに分けられます。ただし、tの値1つに対し、xの値は2つありますので注意。図形的にも考察を加えていれば、(C1とC2の図を書いていれば)間違えることはないはず。
(4)はさらに(3)を利用します。図を書くのは難しいですが、C1とC2の共有点が1個、3個、5個のときを書けば、最小値がaになるのが前者2つのときであると分かりますね。
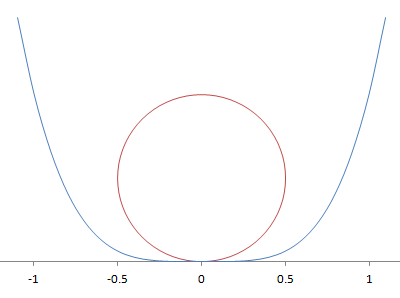
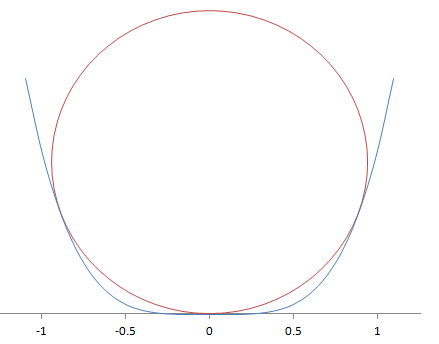
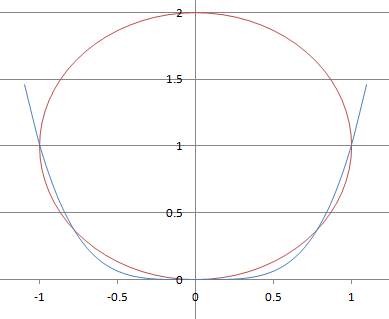
参考までに、ざっくりとした図を載せておきます。順番に、a=1/2、a=A(接する)、a=1のときです。
※KATSUYAの解いた感想
定数入り3次?場合分けの予感するも、範囲のおかげて場合分けなし。そこはメインではいと。(2)は計算するだけ。(3)はおそらく(1)の式が出てくると予想。2乗を置き換えると出てきた、だからt≧0なわけね。図形考察も合わせ、1個、3個、5個を出す。(4)はこの円を考えればいいのね。図がめちゃ書きづらい。あとでPCで書いてみよう(その結果が上です)。解答時間20分。
☆第3問・・・【確率+数列】正三角形上の頂点の移動、確率のシグマ計算(BC、35分、Lv.2)
正三角形の頂点を決まった確率で回る問題です。(1)は例によって誘導だと思いますが、1番や2番ほどは親切ではありません。しかし、これ以上親切にも出来ませんので、(2)は自分で気づいてもらうしかないです。基本的には「BとCの間を永遠とさまよっている」状況が浮かべれば勝ち。
A→BC→BC・・・・BC→A (あるいはBとCが逆) か、A→BC→BC→・・・B→A (あるいはBとC逆)かです。
どちらのパターンかで、奇数回か偶数回かを判断すれば計算できます。
(4)は「2回目」パターン。「初めて」から「2回目」を出す問題は、今年だけでも名古屋大、慶應理工、慶應医などで出題されています。難関大頻出のパターンと言えるでしょう。初めて到達する確率を利用し、シグマ計算をすればOKです。
「k回目で初めて到達 → 残り2N-k+3でまた初めて到達」と考えればOKですね。
※KATSUYAの解いた感想
確率か。n絡みなら漸化式かな?設定と確率を読む。んー違うな、BとCを永遠とさまようだけだわ。ちょっと期待はずれで(2)まではさくっと終了。(3)のパターンは今年よく見る。シグマとればいいか。場合わけしてあるから、式は結構煩雑なので慎重に。解答時間23分。
第4問・・・【積分法の応用】楕円の面積、楕円柱の切断体の体積(B、25分、Lv.2)
楕円柱を切断する問題で、題材としてはそこまで難しい問題ではありません。最近だと円柱バージョンで東北大に出題があります。(年度忘れました)広大での出題は珍しいですが、一度でも経験して流れをつかんでいれば取れますので、本学受験者なら欲しいところ。 なお、楕円であることはほとんど使いませんので、「式と曲線」からの出題はないと言えます。
(1)は楕円の一部を出す問題です。円に相似拡大して出してもいいですし、積分で出してもいいでしょう。積分で出す場合は、asinθとおく置換です。
(2)は、形は長方形です。横(xy平面の線分)と縦(高さ?)縦ます。横は(1)でy=・・・にしていればその2倍、縦は45°の直角二等辺を利用して出せます。これを積分すれば(3)も出せますね^^
なお、(3)の積分計算では、(1)の答えに相当する部分もありますので、そこは結果を借りましょう。残りは、こちらの手法を身につけていると置換すら不要です。
(拙著シリーズ(白) 数学III 積分法 p.14-16)
「第2置換積分」でと書いていますが、それを頭でやってしまおうという算段です。拙著シリーズであれば、やり方を詳しく書いていますし、練習もたくさんあります。
※KATSUYAの解いた感想
柱の切断は典型。楕円ってのが新しいけど、題材としては新しくはない。(3)は(1)の積分が途中で出たので利用。残りも上記方法で行えばすぐに積分できる。解答時間15分。
第5問・・・【整数+ベクトル】内積、1次不定方程式、距離の最小値、格子点の個数(C、50分、Lv.2)
最後は整数+ベクトルです。うまく融合してあるような、無理やりなような、そんな印象を受ける問題です。多分数が大きいからでしょう。
(1)は内積で聞いていますが、ただの1次不定方程式です。最初の解として何を見つけるかによりますが、x=ー1、y=4を見つけておくと後が結構楽かもしれません。 自然にやると6とー21が出そうですね。
(2)は(1)を利用して一般解を出しましょう。距離なので2乗して平方完成しますが、軸に一番近い整数が知りたいだけなので、頂点のy座標部分の計算は不要です。
初期解を(ー1、4)として(ー1+7k、4-25k)で設定しておくと最も近いものから順にk=0、1、ー1、2、ー2、3・・・と、軸をはさんで左右交互に現れます。偶数番目が1、2、3、・・・と綺麗にに並ぶので、(3)がやりやすいですね^^
(4)は(3)ができれば出来るはず・・・ですが座標が「大きすぎて正確にかけない+細かい部分を知りたい」という相反する状況もあり、難しいと思います。ここは捨てても問題ないでしょう。
できる四角形は平行四辺形ですが、長い線には途中に2つ格子点があります。頂点と合わせると8個です。聞き方からしてこの8個しなかないのでしょうが、それを証明するところが大きな壁になりそうですね。
予備校さんの解法を見たところ、2つとも私と違いました。
K塾さんは、「格子点で囲まれる図形の面積が1なら、内部に格子点がない」ことを利用しています。かなりスマートですが、高度な発想です。
S台さんは直線y=nと平行な2直線との共有点条件として証明しています。発想、計算量ともにスタンダードと言えます。
私は大きな長方形から三角形4つと長方形2つに含まれる格子点を引いて、強引に8個しかないことをまずは示し、実際に見つかった8個が全てである、と結論づけました。計算量が多く、最も泥臭いやり方ですが、最も発想のいらないやり方です。
様々な解法を学び、発想的にはどうか、計算量的にはどうか、といったことを意識しながら身につけていくと、本番でも状況に応じて解法を選ぶことができると思います。
※KATSUYAの解いた感想
今年も最後が整数ね。(1)(2)はただの1次不定方程式。具体解から一般解へ。(1)で(x、y)=(6、ー21)にしていたが、(2)の距離の式が(さらに平方完成すると思うと)メンドウな気がする。(1)を(ー1、4)に変更してやり直し。まだマシになった。(3)は(2)で修正しておいたよかったと思った。偶数番目がきれいに1、2、3・・・と並ぶ。(4)は難しいかも。てか、数値デカイし。。。全て求めよってことは、多分そんなにないんやろな。とりあえず8個は確実にあるけど、これ以外にないことをどう言えばいい?数値もでかく、直線の式を出してみる。2つの直線は思ったより近いからやっぱりないんやろな。しかしこれ以上は進まず。いいや、強引に長方形から引いていくか。計算して8個になったので、見つけた8個が全てになると分かり終了。解答時間35分。最後は捨てても大丈夫やろなー。
4.対策
広島大は、やることは典型的ですが、融合問題が多い印象です。問題にあたっていく中で、「これを使えばいい」と判断できる力が必要です。手法自体は、青チャートで十分網羅できていますので、まずは手法を一通りマスターし、その上で融合問題を多く解く演習をしましょう。数学IIIの計算はもう少し複雑なことが多いので、微積で計算練習を怠らずに。
量をこなす演習:じっくり演習=7:3でOK。
以上です^^
■他年度の、本大学の入試数学■
>> 2015年度
>> 2016年度
■関連する拙著シリーズ■
★ 数学II 三角関数 (第1問)
★ 数学II 微分法 (第2問)
★ 数学B ベクトル (第5問)
★ 数学B 数列 (第1問、第3問)
★ 数学III 極限 (第1問)
★ 数学III 積分法 (第4問)
★ 数学III 積分法の応用 (第4問)
分野を見ていると、極めてバランスの良い出題であると分かりますね。
★ 計算0.9【IAIIB】 (計算練習帳です^^)