センター試験数学II・B【2007年】の難易度、傾向は？

2014/05/23 2016/12/18

本エントリーでは、2007年に行われたセンター試験数学IIBの難易度や傾向に関する情報についてまとめています。

【評価指標】

１．難易度　A(易)～E(難)

２．パターンレベル
Lv.１(習得していて当たり前)
Lv.２(習得していないと、差をつけられる可能性がある)
Lv.３(習得していなくてもしょうがない)

３．解答するまでの標準的な時間

です。これら３点から、各問題ごとにコメントしていきたいと思います。

センター試験数学Ⅱ・B（２００７年）

０．2007年のセンター試験数IIBの平均点

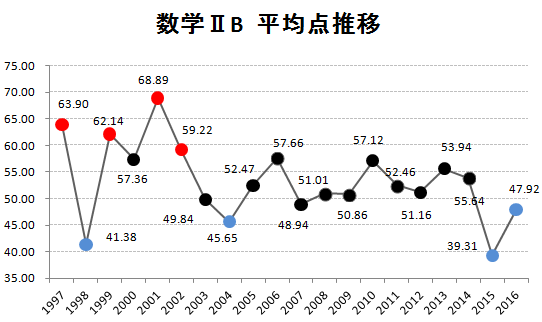
まずは、1997年からの平均点推移を掲載しておきます。赤丸は平均点の高かった年ベスト４、青丸は平均点の低かった年ベスト４です。

（データを元にKATSUYAが作成　グラフの転載可）

今回の2007年は48.94点で、過去20年間でワースト５の年になっています。

１．総評～計算量は少なめ。数Bの難しさに引っ張れて全体的にも難～

必須の数IIは普段より計算は少ないものの、毛並みが少し変わった問題も散見。第３問の数列は後半の誘導の意図が読み取りにくく、計算も煩雑。第４問のベクトルも文字が乱立するパターンで、誘導と図形的意味を結びつける必要有り。全体として数Bの難に引っ張られ、やや難。

※KATSUYA個人としては、ワースト５になるほど難とは思えませんでした。

■目標解答時間・・・・８０分

2009年の第２問の場合分けのような問題がありませんので、特定の問題に時間がかかることはなさそうですが、数Bの数列は悩みどころと計算の煩雑さが目立ちます。

２．各大問の難易度

第１問[1]　(三角関数、倍角、加法定理、不等式、AB(例年比やや易)、１０分)

三角不等式を題材とした、三角関数の問題。不等式はシンプルですが、誘導から何をすればよいかやや見にくいです。sinx、cosxを用いて表すには、左辺は倍角、右辺は加法定理で展開するしかありません。

三角方程式、不等式においては、角度を統一することが最優先となります。θに統一する、という方針です。

Principle Piece Ⅱ-65

統一すべきは「種類」か「角度」

（Principle Piece 数学Ⅱ 三角関数　p.46）

「左辺の因数分解を利用して」というのは逆に誘導過剰かと思われますが＾＾；

（2sinxー１）（２cosx＋１）＞０　という形になった場合は、「両方正」または「両方負」という考え方で範囲を出しましょう＾＾

第１問[2]　(対数不等式(底で場合分け)、底の変換、領域、B(例年並み、新傾向)、１４分)

前半同様、不等式を題材とした問題。底が「y」という文字になっていることから、底の大小でｌｏｇ_y　を外すときの不等号の向きも変わります。　この手のタイプの問題は、類題経験がないと難しいです。

底の変換や式変形は、誘導に従えばできるでしょう。「タ」を含む式は、右辺第２項も底の変換をし、全体を２で割れば見えてきます＾＾

最後の領域は、y＝１を境に、領域の上下が変わります。どちらが上で、どちらが下か、落ち着いて答えましょう。

第２問 (微積総合、最大値、面積、接線、なす角、BC(例年比やや易、新傾向)、２０分)

2007年の微積は、計算量は割と穏やかだったっと思いますが、最後のなす角はあまり聞かれたことがなく、戸惑ってしまったかもしれません。

前半は共有点がある条件と、２次関数の最大値、数Iの範囲で解決できてしまいますね。g（x）の計算を間違えると全滅しますので、慎重に。

後半は３次関数の最大値、および面積、接線で、こちらは数学Ⅱの範囲ですが、普段より計算量も少なく、比較的スラスラ解けたのではないかと思います。

３次関数どうしの領域の面積でも、x＾３の項が消えれば、こちらの原則が使えますね＾＾

Principle Piece Ⅱ-112

放物線とx軸の面積　a/6 (α-β)^3　の利用

（Principle Piece 数学Ⅱ 積分 p.29）

最後のなす角は珍しい問いですが、２直線のなす角については、こちらの原則を用います。問題文にtanとありますし、思いつくのは難しくはないでしょう。

Principle Piece Ⅱ-60

なす角はtanの加法定理で攻める

（Principle Piece 数学Ⅱ 三角関数 p.34）

第３問 (漸化式、和の計算、階差数列、B(例年比やや難、新傾向)、２５分)

この年の数列は数列の計算を強いられるところはあまりなく、誘導を読み取れるかどうかの要素が非常に強い問題で、取り組みにくかったと思われます。
（１）は、漸化式をノーヒントで解かせる問題。このタイプであれば教科書にもありますから、ここはノーヒントでもできなければいけません。

Principle Piece B-11

an+1=pan+q 　c＝pc＋q　なるcを出す

（Principle Piece 数学B ベクトル pp.6）

一般項が出れば、和は簡単に出せますね＾＾　最小となる自然を求めるところが、意外と詰まったかもしれません。Sn＞０を少し変形して、３＾nー１>45n　としておくといいでしょう。３^nの方が急激に大きくなりますから、小さい数字を入れていくといいです。n=4 だとぴったしなので、答えは n＝５です。注意。

問題は後半。最初に聞かれているのは「bn＋cn」です。うまく敷変形すれば出来るのかと思いきや、できません。結局最後には「bn」、「cn」の両方を聞かれていますし、この時点でbn、cn についての連立方程式を解いて、素直にその2つを足すとよかったです。なおここで詰まると、ここから先は全滅となります。

その後、その数列の階差数列を出します。階差数列は与えられていますからいいですが、これとanが一致することを利用して、d、r、xを全て出さなければいけません。文字が３つなので、n＝１、２、３を代入した式を作ると良かったと思います。差をとれば３d／５　の項は消えますし、等比の部分は、（１－r）、（１－r^2）などが差となって現れます。ここだけ見れば、r→x→dの順番に出ます。
文字が多いことに加え、あまりセンターで用いることのない手法なので、難しかったかもしれません。

第４問 (空間座標、内積、内分・外分、空間上の２直線の交わり判定、B(例年並)、１５分)

４点座標型の空間ベクトルです。４点が与えられているので四面体系統かと思いきや、そうではありませんでした＾＾；

内分点を多く聞かれますが、（１－●）：●でどんどん解決します。センターに限らず超頻出手法ですから、スラスラできるようにしておきましょう。OGベクトルは、E、Fの座標を先に表してから同じく内分点を取ります。
後半ですが、OGとBCの交わり判定の問題です。空間上では２直線は交わるとは限りませんので、交わるように「b」、「s」を決めなさい、ということです。

２直線の交わりについては、こちらの原則が聞いてきます。平面ベクトルの原則ですが、もちろん空間でも使えます＾＾

Principle Piece B-35

交点を求めるなら
s●→＋(１－s)■→　を2つ作って連立

（Principle Piece 数学B ベクトル pp.34～35）

今回は、直線のうちの１つがOGと、Oを通っていますので、OHベクトルはOGベクトルの実数倍とおけます。BC上の点については、BH＝sBCとおいてありますが、結局OH=OB＋sBC＝（１－s）OB＋sOC　となりますので、上の原則を用いているに過ぎません。
３成分が一致することを利用して連立方程式を解くことで、s、t、bは全て出せます。

最後の外分点ですが、s＝３／２をOHベクトルに代入し、OH=ーOB＋３OC／２＝ーOB＋３OC／（３－１）　とすれば、３：１に外分するとわかりますが、外分は分かりにくいので、図も一緒に書いていきましょう。