センター試験 数学II・B【2006年】の難易度、傾向は?
2016/12/18
本エントリーでは、2007年に行われたセンター試験数学IIBの難易度や傾向に関する情報についてまとめています。
【評価指標】
1.難易度 A(易)~E(難)
2.パターンレベル
Lv.1(習得していて当たり前)
Lv.2(習得していないと、差をつけられる可能性がある)
Lv.3(習得していなくてもしょうがない)
3.解答するまでの標準的な時間
です。これら3点から、各問題ごとにコメントしていきたいと思います。
センター試験数学Ⅱ・B(2006年)
(複素数平面は2015年以降のセンター試験には出ないので、評価は割愛いたします。)
0.2006年のセンター試験数IIBの平均点
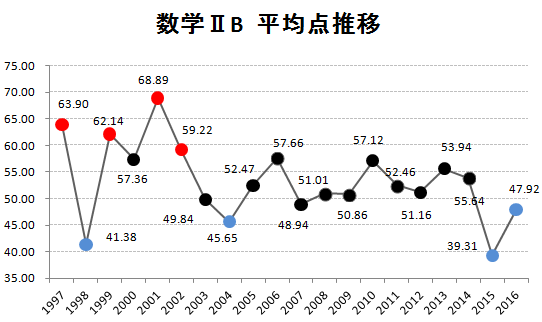
まずは、1997年からの平均点推移を掲載しておきます。赤丸は平均点の高かった年ベスト4、青丸は平均点の低かった年ベスト4です。
(データを元にKATSUYAが作成 グラフの転載可)
今回の2006年は57.66点で、過去20年の中では例年並みか少し高め、といったところでしょうか。
1.総評~数列はIAのときと少し毛色が変わるが、全体として並~
指数対数三角はやや易。第2問の微積は共通接線という題材ですが、誘導が丁寧でやや易。
【2006~2014の課程】初めて数学Bへ移行した数列。数学Aの数列のときよりも計算量がすくなく、やや易。第4問のベクトルはやっていることを理解しにくいが、素直についていってとけば出来、並。
【~2006の課程】ベクトルはやっていることを理解しにくいが、素直についていってとけば出来、並。最後の出題となった複素数平面は、文字が乱立するが、落ち着いて把握すれば計算量は少なめで並。
■目標解答時間・・・・75分
全体的に計算量が例年より少なめで、穴埋め形式であれば時間には少し余裕があったのではないでしょうか。
第1問 [1] (三角関数、倍角、加法定理、不等式、AB(例年比やや易)、10分)
三角関数の最大・最小の問題。2次関数と絡むパターンで、定義域がー1~1を取ることに注意すれば、どうってことはありません。最後はcos αの値が出ればsin α の値も出ますので、加法定理の展開に必要な値は全て得られますね^^
cos2θを倍角で変形する公式はセンターでは頻出です。sinだけが残るように変形しましょう。
(Principle Piece 数学Ⅱ 三角関数 p.46)
第1問[2] (対数関数、対数不等式(底で場合分け)、底の変換、領域、B(例年比やや易、新傾向)、12分)
対数は、2006~2008年の3年連続で不等式です。また、底が「x」という文字になっていることから、底の大小でlog_x を外すときの不等号の向きも変わります。 この手のタイプが、2006年、2007年と続いています。
真数にもあり、底にもあることから、x>0かつx≠1 です。バカにされているような穴埋めですが、最後の条件には非常に大切です。サービス問題と思って受け取りましょう^^
次は底が変わっていますので、底の変換公式を使えばOKです。対数は公式が多いので、何の式変形か判断できるようになりましょう。
最後は、xの大小で場合わけです。0<x<1のときは、不等式の両辺にlog_3 x をかけるときに不等号の向きが変わるので、注意。
第2問 (微積総合、共通接線、面積、B(例年比やや易)、16分)
2006年の微積は共通接線が題材ですが、誘導は割と丁寧で計算量も割と穏やかだったので、易しめかと思われます。
誘導にあるように、放物線と放物線の共通接線の場合は、片方における接点のx座標を「t」とおいて接線の方程式を出し、それがもう片方に接する条件を判別式で求めるといいでしょう。
(Principle Piece 数学Ⅱ 積分 p.29)
後半は小問がバラバラと並んでいますが、前半ができればほぼ芋づる式にどんどん求められます。最後の面積は「a」が入ったままで少々ややこしいですが、解答の形から因数分解できる形になることは目に見えていますので、それをヒントに計算すればOKです。
第3問 (等差中項、等比中項、等比数列の和、階差数列、B(例年比やや易、新傾向)、14分)
2006年より数列が数学Bとなりました。ⅡBとして初めての数列は、数学Aのときの数列より穏やかでした。しかし、前半の等差中項、等比中項は手法を覚えていないと詰まってしまうでしょう。等差中項からは 2b=a+c、等比中項からは a^2=bc が出来ます。これで、b、cをaで表すことができますね^^
これにより公差、公比ともにわかりますから、(2)まで解けます。
(3)は、「階差数列→元の数列」の順番の典型的な求積です。「a」が最後まで入っていますが、あまり計算は複雑ではありませんね。
第4問 (平面ベクトル、内積、なす角、領域と最大・最小、B(例年並)、15分)
2006年のベクトルは平面ベクトルです。まず、平面ベクトルは、2つのベクトルが基本になります。本問では、a、bベクトルを基本ベクトルとしていく方針です。まずそれを見抜きましょう。
(1)の最初は内積を出させています。これにより、基本ベクトルの長さおよび内積が両方でましたので、これ以降は「何を聞かれても基本的に怖くないはず」と思えれば安心ですね^^
(Principle Piece 数学B ベクトル pp.22~24)
従って、「2a+b」ベクトルの長さも、なす角も怖くありません。
(2)では、cベクトルをa,bで表す問題ですが、もちろんsaベクトル+tbベクトル とおいて、s、tに関する方程式を作ります。1つは、cの長さが1、1つはa,cが垂直であることです。 「s、t」の導入は基本ベクトルで表すときの典型手法のはずですが、これを思いつかなかった人も多いようです。
(3)は、(2)ができれば大したことはないはずです。√3がつきまとうので、計算はミスを誘発しそうですが、条件の不等式はただの1次不等式ですから、直線で囲まれた領域です。 最後は領域内の最大・最小です。直線で囲まれた領域なので、端点か交点のいずれかとなりますね^^
(Principle Piece 数学II 図形と式 pp.59~60)
3.センター試験対策
レベル的には、教科書の章末問題レベルです。そのレベルの問題を、いかに素早く解くかがカギになってきます。従って、計算力がものを言います。どの単元も、まんべんなく少しずつ問われますから、すべての計算を素早く計算する習慣を普段から身に付けておいてください。
2次で数学がいる人は、特に意識する必要はありません。2次の対策がそのままセンターの勉強になってます。過去問や模試などで、形式になれることだけしておくといいでしょう。
■関連するPrinciple Piece■
・Principle Piece 数学Ⅱ 三角関数
・Principle Piece 数学Ⅱ 図形と式
(第1問[1]対応)
・Principle Piece 数学Ⅱ 指数・対数関数
(第1問[2]対応)
・Principle Piece 数学Ⅱ 微分
・Principle Piece 数学Ⅱ 積分
(第2問対応)
・Principle Piece 数学B 数列
(第3問対応)