センター試験 数学I・A【2008年】の難易度、傾向は?
2016/12/18
本エントリーでは、2008年に行われたセンター試験数学I・Aについて、難易度や傾向などの情報についてまとめています。
【評価指標】
1.難易度 A(易)~E(難)
2.パターンレベル
Lv.1(習得していて当たり前)
Lv.2(習得していないと、差をつけられる可能性がある)
Lv.3(習得していなくてもしょうがない)
3.解答するまでの標準的な時間
です。これら3点から、各問題ごとにコメントしていきたいと思います。
センター試験数学Ⅰ・A(2008年)
0.2008年のセンター試験数IAの平均点
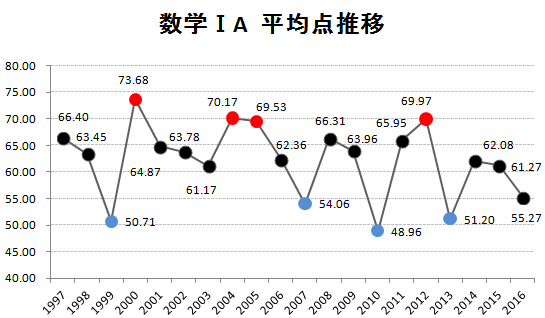
まずは、1997年からの平均点推移を掲載しておきます。赤丸は平均点の高かった年ベスト4、青丸は平均点の低かった年ベスト4です。
(データを元にKATSUYAが作成 グラフの転載可)
今回の2008年は66.31点となっており、例年に比べてやや高めの平均点となっています。
1.総評~2次関数・確率は易。三角比と平面幾何の融合はやや難。
第2問に軸分けがなく易しい。第3問は相似比と方べきの定理の併用があり、少し難しめ。第4問の確率は全事象が少なく書き出しで解決可能。全体として平年並み。
第1問は2次不等式を解くだけで、ラク^^。後半の必要十分も比較的ラク。
第2問の2次関数は、主軸の「場合分け」「解の存在範囲」が両方なしで、誘導に従って順番に解けばできます。
第3問もいつもどおりの三角形と外接円、内接四角形。後半の平面幾何との融合は設定は単純だが、相似比と方べきの併用を要求されています。
第4問の確率は全事象が少なく、落ち着いて書き出せば解答可能。逆にあまり公式を使うところがなく、地道に調査した人の勝ち。
■目標解答時間・・・・55~65分
第1問、第2問ではいつもよりも時間をかけずに住んだと思います。その分第3問にかけることができれば、高得点が望めるセットでしたね。
2.各大問の難易度
第1問[1] (点の移動、2次不等式、A(例年より易)、5分)
点の移動の問題は、中学生の数学によくあったかと思いますので、ここは大丈夫でしょう。2次不等式もいたって基本で、ここはラクでした。
KATSUYAの感想
特につまるところはなし。解答時間1分。
第1問[2] (必要十分・包含関係 AB(例年並み)、6分)
3つの実数の範囲の集合に関する問題です。倍数系の条件は、頑張って証明をしようとせずに、いくつか当てはめてみましょう。偽のときに、普段から反例を2、3個見つける練習をしておくと、偽の臭いをかぎ取れるようになれます。
KATSUYAの感想
まずはいくつか書き出しで判断。本当にそうなるかどうか、論理的にも考えて終了。解答時間4分。
第2問(頂点、x軸との交点、最大・最小、AB(例年並み)、15分)
例年通りいろいろと聞いてきますが、今回は少し「雑」と言えるぐらい、雑問の寄せ集めという印象で、ただただ聞かれていることに従って解いていくだけです。
頂点の座標が分数式になることにより計算が全体的に少しメンドクサイですが、場合分けなどもなく、ラクな2次関数でした。
第3問(外接円、内接四角形、正弦・余弦、円と直線、面積など、例年比やや難、20分)
いつも通り、三角比+平面幾何の融合問題です。前半では、余弦定理の2次方程式型に帰着させるタイプ(原則あります^^)があり、いつもに比べるとやや難。
余弦定理の基本は、「2辺夾角がわかっているときに、残りの辺の長さを求める」です。しかし、ADを求める際には、こちらの原則を用いる必要があります。
(Principle Piece 数学I 三角比 p.24)
分かっている角度は、∠ADC=45°(円周角の定理)ですから、AC^2=・・・ の式を立ててADに関する2次方程式を解くことになります。
後半の最初は接弦定理を利用すれば相似が見えます。最後は、相似比と方べきの定理を活用する問題です。相似比の値も活用するので、こちらもやや難レベルになっています。
(Principle Piece 数学A 平面図形)
こちらの原則の意味は、方べきの定理の式をただ立てるだけではなく、どの三角形とどの三角形の相似によって言えることなのかを、しっかり把握しよう、ということです。そして、3辺の比を並べておきましょう。
実際にKATSUYAが解いた方法を示しておきます。
↓↓↓↓↓↓↓↓↓↓↓↓↓
CE=x、AE=y とする。
ACE∽DAE
AD:DE:EA=CA:AE:EC
すなわち
3√5:(√10+x):y=5:y:x
3√5:y=5:x なので、y=3√5/5 x
(√10+x):y=y:x より
y^2=x(√10+x)
下線部を代入して xで割り、整理して x=√10×5/4
下線部に入れて y=15√2/4
↑↑↑↑↑↑↑↑↑↑↑↑↑↑
第4問(場合の数、確率、サイコロの目と規則、B、例年並み、14分)
確率は、サイコロの出た目に応じてA,Bを書いたり削除したりする問題です。全事象がそこまで多くないので、慎重に書き出せば解けたと思います^^
ポイントとしては、2文字で終わるためには、最初に「5、6」、あとは「1、2、3、4」が出ないとダメだと気づくことです。文字を書いてから削除すると、多くても1文字しか残りません。
文字列がAで終わるには、××A、A×A、B×A、AA×、AB× であればOKです。×の数で分けるといいでしょう。Bで終わる確率もAと同じだけあるはずですから、1文字の確率も一緒に出せて、期待値に使えますね^^
※「ここはこんな風に考えて出した!」という人は、どんどんコメントください。数学は、他の人の解き方を聞くことで伸びる科目です^^
3.センター試験対策
レベル的には、教科書の章末問題レベルです。そのレベルの問題を、いかに素早く解くかがカギになってきます。計算力がものを言います。どの単元も、まんべんなく少しずつ問われますから、すべての計算を素早く計算する習慣を普段から身に付けておいてください。
2次で数学がいる人は、特に意識する必要はありません。2次の対策がそのままセンターの勉強になってます。過去問や模試などで、形式になれることだけしておくといいでしょう。
【必読!! 新課程で受験する皆さんへ】
第3問のような、平面図形と三角比の融合は2015年度センター試験には出ません。みなさんが受ける試験は、数学Ⅰから「三角比」のみ、数学Aから選択で「平面図形」のみとなります。ですので、過去問の第3問で取れなかった人は、悲観するには及びません。 なお、期待値も出ませんが、条件付き確率は出ます。
■関連するPrinciple Piece(2016年度、新課程に合わせた内容に対応しています)■
・Principle Piece 数学Ⅰ 方程式と不等式
(第1問[1] 対応)
・Principle Piece 数学Ⅰ 2次関数
(第2問対応)
・Principle Piece 数学A 論理と集合
(第1問 [2] 対応)
・Principle Piece 数学Ⅰ 三角比
(第3問対応)
・Principle Piece 数学A 集合と場合の数
(第4問対応)
・Principle Piece 数学A 確率
(第4問対応)
・Principle Piece 数学A 整数
(新課程では出題されます!)
・Principle Piece 数学A 平面図形
(第3問対応)
Principle Piece 数学IA 原則のみ
(全問対応)
センター試験対策用の参考書については、こちらのリンクからどうぞ^^