センター試験数学II・B【2008年】の難易度、傾向は？

2014/08/18 2016/12/18

2009年に行われたセンター試験数学IIBについて、難易度や傾向に関する情報についてまとめていきたいと思います。

【評価指標】

１．難易度　A(易)～E(難)

２．パターンレベル
Lv.１(習得していて当たり前)
Lv.２(習得していないと、差をつけられる可能性がある)
Lv.３(習得していなくてもしょうがない)

３．解答するまでの標準的な時間

です。これら３点から、各問題ごとにコメントしていきたいと思います。

センター試験数学Ⅱ・B（２００８年）

０．2008年のセンター試験数学IIBの平均点

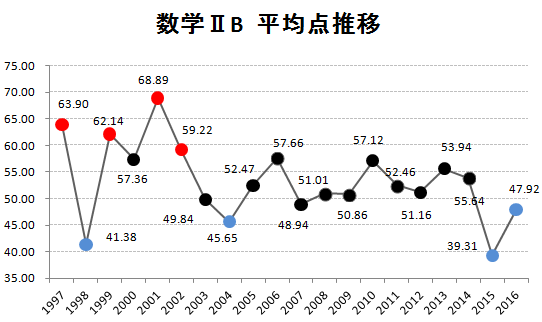
まずは、1997年からの平均点推移を掲載しておきます。赤丸は平均点の高かった年ベスト４、青丸は平均点の低かった年ベスト４です。

（データを元にKATSUYAが作成　グラフの転載可）

今回の2008年は、51.01点となっています。点数から見ると、難しい年のグループに入りそうです。

１．総評～数学IIが例年より難しく、数Bは点数が取りやすい。

必須の数IIでは第１問が全体的に新傾向。第２問は面積に場合分けが必要でセンターとしてはかなり難。ただし、第３問、第４問が普段より複雑でなく、点数が取りやすく、全体の難しさが緩和。

第１問の前半の指数・対数は、指数に対数が入っているタイプ。後半の三角関数は、図形的な要素も絡み、良問だが少し難しめ。

第２問の微積は例年よりかなり難。面積には場合分けが存在する。穴埋めの形などからなんとか予想できそうだが、場合分けの計算がないと難しい。計算量も多い。

第３問は漸化式の計算であるが、誘導がわかりやすく、計算量も最後まであまり多くない。

第４問のベクトルは６辺から内積を3つ求めて垂線、面積、体積という、典型的なパターン。数値設定も親切で、普段よりやや易。

■目標解答時間・・・・７５～８５分

第２問の場合分けは、２次で聞かれてもおかしくないレベルで、ここで時間を取られるかもしれません。第１、２問は難しく、詰まったときに早めに第３、４問に移れたかどうか。

２．各大問の難易度

第１問[1]　(指数・対数、最大・最小、相加・相乗、AB　例年並み　新傾向　１０分)

対数式の最大、最小を求める問題です。条件式、求める式ともに指数部分に対数が入っており面食らったかもしれませんが、誘導に従っていけば最後まで問題なく解けます。

z＋１／ｚ　の形は、センターⅡBではお馴染みで、相加相乗の利用です。だいたいここで出てきますので、アンテナを張っておきましょう。

Principle Piece Ⅱ-6

x＋●／x　の形は相加相乗の利用

（Principle Piece 数学Ⅱ 式と証明）

第１問[2]　(三角関数、図形、扇形の面積、加法定理、周期、AB、やや難、新傾向、１３分)

2008の三角関数は２つの円を絡めた図形問題です。三角関数の最初に習う扇形の面積などを聞かれていますが、問題の意図をきちんと読み取らないと答えられません。

後半は、答案の形からも予想が付きますが、加法定理の展開式に気付いて戻せるかどうかがポイントとなります。

Principle Piece Ⅱ-59

条件式を２乗して加法定理の展開式を出す

（Principle Piece 数学Ⅱ 三角関数　p.33）

という原則がありますが、逆に２乗された式には加法定理の展開式が現れるということになりますね＾＾

最後の周期は盲点とならないように。周期が普段の２倍なので、角度は普段の半分になります。

第２問(微積総合、接線、面積計算、面積関数(場合分け)、最大・最小BC、例年比難、２５分)

2008年の微積は、２つの放物線を題材とした問題で、後半はかなりハイレベルでした。

まず前半は共有点、接線、基本的な面積計算を聞いています。ここはしっかりと確保していきたいところです。放物線とx軸で囲まれた部分の面積は、もちろんこちらを利用します＾＾

Principle Piece Ⅱ-112

放物線とx軸の面積　a/6 (α-β)^3　の利用

（Principle Piece 数学Ⅱ 積分 p.29）

さて、問題は後半です。まずは、求めようとしている面積がいったいどこなのかをきちんと把握する必要があります。ヒントになっているのは、３行目と６行目です。

まず３行目について。
０＜ａ≦「タ」　のとき　S（ａ）＝ー「セ」／「ソ」a^3+「ケ」／「コ」

となっており、S(a)は直前で求めた面積の差となっています。すなわち、求めた部分がx＝０～x＝２の範囲に完全に入っているということです。ａ～２ａの部分が完全にこの範囲に入るには、２ａ≦２、すなわち、ａ≦１　と分かります＾＾

また、６行目もヒントになります。
「チ」＜ａ　のとき　S（ａ）＝「ケ」／「コ」

すなわち、このときはC１とy軸、x＝２で囲まれる部分そのものになっています。C2が関わってこないということは直前で求めたC2の部分が、この領域にないということです。ａ～２ａの部分がここから外れなければいけませんので、２＜ａ　と決まります＾＾

すると残りの場合分けは１＜ａ＜２となりますので、この場合の図を丁寧に書く事で、残りも面積を求めることができます。この場合の面積も出せれば、最後の最小値も出せます＾＾

センター試験でこの手の問題は、60分という制限時間を考えると、結構酷な問題ですね＾＾；

第３問(等差数列の一般項とその和、漸化式、Σ計算、B、例年比、新傾向、２０分)

2008年の数列は例年より煩雑さがなく、解きやすいです。最初の等差数列とその和は、人によっては暗算レベルでしょう。

（２）からは、漸化式の問題です。最初の b＿n は何をするためのものかよく分からない段階ですが、恒等式と見て係数を合わせるだけです。

c_nの段階になると、b＿nの意味が見えてきます。c_nとb_nは同じ漸化式ですから、d_nのように置けば、d_{n+1}-2d_n=0となることは想像に難くないでしょう。

あとはd_nを等比数列で求め、＋b_nすればｃ_ｎが出ます。最後のΣ計算は、等比部分と２次式部分に分けて計算しましょう。