センター試験 数学I・A【2010年】の難易度、傾向は?
2016/06/27
2010年に行われたセンター試験の数学I・Aに関する情報についてまとめていきます。
【評価指標】
1.難易度 A(易)~E(難)
2.パターンレベル
Lv.1(習得していて当たり前)
Lv.2(習得していないと、差をつけられる可能性がある)
Lv.3(習得していなくてもしょうがない)
3.解答するまでの標準的な時間
です。これら3点から、各問題ごとにコメントしていきたいと思います。
センター試験数学Ⅰ・A(2010年)
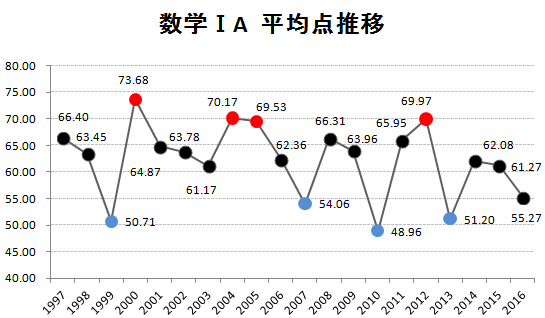
0.2010年のセンター数I・Aの平均点~過去20年で最低~
まずは、1997年からの平均点推移を掲載しておきます。赤丸は平均点の高かった年ベスト4、青丸は平均点の低かった年ベスト4です。
(データを元にKATSUYAが作成 グラフの転載可)
今回の2010年は、過去20年間の中で最低の平均点となっています。
1.総評~全体的に点数を落としやすい。
例年に比べると全体的に点数を落としやすい部分が多く、平均点についても納得の難しさだと思います。
第1問の計算は、√ を含む数字の大小を聞かれています。後半の必要・十分も「証明せよ」と言われると非常に書きにくく、ある程度の直感も必要。
第2問の2次関数は、主軸の「場合分け」、「解の存在範囲」がともになく、こちらは取りやすかったかと思われます。最後は、頂点が y=x+5 上にあればよいと気づけばラク。
第3問の図形は難易度的には変化なしと見受けられますが、外接円でなく内接円がネタになっており、本番で慌てた可能性もあり。計算量や使うネタは普段と同じで、落ち着いて図を書けば取れたハズ。
第4問の確率は難化。期待値の計算自体は簡単だが、そこまでが普段より誘導がかなり不親切なため答えにたどり着けず、下手すると最初以外全滅も有り得たでしょう。
■目標解答時間・・・・65~75分
答案まで作成していけ、と言われるとこれぐらいの時間がかかるとは思いますが、第3、4問などは方針が立たないとお手上げ。いじくっている間に時間が過ぎてしまったかもしれません。
2.各大問の難易度
第1問[1] (有理化、2次方程式、大小、AB、8分)
前半は基本的な有理化と2次方程式です。最後の大小は慣れていないと少し難しいでしょうか。
5ー√21/2 と 1/6 の大小ですが、√を含む大小を比較するときは、√ を単独にしてから2乗します。
(5ー√21)/2 と 1/6
↓
5/2ー1/6 と √21/2
↓
7/3 と √21/2 ここで2乗
↓
49/9(=5.44・・・) と 21/4(=5.25)
大小がわかったら、今後は逆に辿ります。
(5ー√21)/2 > 1/6
↑
5/2ー1/6 > √21/2
↑
7/3 > √21/2
↑
49/9 > 21/4(=5.25)
KATSUYAの感想
特につまるところはなし。大小関係は上のとおり。解答時間2分。
第1問[2] (必要十分・包含関係 B、8分)
集合が4つあります。1つ1つの条件はわかりやすいですが、「かつ」で合わさるとどうなるのか、わかりにくかったかもしれません。
センター試験は答えだけなので、各集合について10個ぐらい書いておくと、直感でもある程度答えが見えます。
P:1、6、11、16、21、26、31、36、41・・・
Q:1、11、21、31、41、51、61、71、81・・・
R:1、3、5、7、9、11、13、15、17、19・・・
S:3、5、7、11、13、17、19、23、29、31・・・
「PかつR」:1、11、21、31、・・・ →Qと同じ
R否定:2、4、6、8、10、12、14、16、18、・・・
S否定・・・1、2、4、6、8、9、10、12、14、15、16、・・・
などです^^ センターでは、5、6個探して反例がなければ、真とみなしていいと考えておくといいと思います。ただし、探し方は、「なるべく反例になりそうなものを探すこと」です。
KATSUYAの感想
まずはいくつか書き出しで判断。本当にそうなるかどうか、論理的にも考えて終了。解答時間4分。
第2問 2次関数(頂点、最小値、x軸との交点、平行移動、AB、15分)
2010年の2次関数は穏やかでした。aにいろんな値を代入したりするなど、手間は多少ありますが、軸分けの問題や解の存在範囲の問題などもなく、点を取れるところでした。
なお(1)、(2)に共通で、G2の頂点はG1上にあります。どの設定がどこまで用いられるのか、要注意です。
最後は平行移動なので、y=f(x-p)+q を用いるのが標準的な解き方です。
しかし、x軸方向にもy軸方向にも同じだけ平行移動するので、もともとの頂点が(ー1、4)にあることを考えると、y=x+5上にあればいいことになります。
従って、G1とy=x+5の交点のうち、x=ー1でない方がもう一つの頂点となりますね^^
第3問(内接円、正弦・余弦、円と直線など、20分)
旧課程でお馴染みの奇問である、三角比+平面幾何の融合問題です。普段は三角形とその外接円上にもう一点とって、内接四角形のようなネタが多いですが、2010年は内接円でした。
内接円ということもあり、少し手間取ったかもしれませんが、3辺がわかっている場合に頂点-接点間を出すのは、常識としておきたいところです。
(Principle Piece 数学A 平面図形 p.40-41)
さて、QRは△ARQに余弦定理を用いれば出すことができます。同じようにしてPR、PQを全て出せば△PQRは3辺が分かりますので、cos → sin の順番でどこでも出せますね^^
(Principle Piece 数学Ⅰ 三角比 p.22-23)
さて、後半は円Oと直線APが2点P,Sで交わっています。この設定で、そのあと聞かれているのが長さになりますので、やはり方べきの定理を視野に入れたいところです。
APは3平方で、SPは方べきで AP・AS=AR^2 を用いると簡単です^^ ここで、AS:SP=2:3 であるということに気づいておかないと、ここから先は難しいでしょう。 ピラミッド型相似を使えば、HPとSHは一瞬です。
tan を聞かれたことも、受験生のペースを狂わせたかもしれません。tan に関する定理はありませんので、一番最初に定義で習ったように直角三角形を見て、SH/CH と見るのが素直です。
最後は、TがCS上にあることに気づけばできます。等しい角度をどんどんマークしてたどっていきましょう。
第4問(場合の数、確率、玉の取り出し方、B、例年比やや難、16分)
たまの取り出し方に関する場合の数と確率の問題ですが、誘導が例年より不親切で、明暗を分けたかもしれません。最初以外全滅という可能性も。
0点のときの考え方としては、以下のようになります。
黒あり
[1] あと4個の数字は1、2、3、4、5から4つ 5通り
[2] 各数字の色は赤、白の2通りあるので、2^4=16通り
5×16=80
2次対策まで行っていればこの程度の考え方は対して難しくはないと思いますが、センターの問題としては上の[1]、[2]ぐらいの誘導があってもよさそうな感じですので、普段より難しかったかもしれませんね。
※「ここはこんな風に考えて出した!」という人は、どんどんコメントください。数学は、他の人の解き方を聞くことで伸びる科目です^^
(承認制なので反映までに時間がかかります。ご了承ください)
3.センター試験対策
レベル的には、教科書の章末問題レベルです。そのレベルの問題を、いかに素早く解くかがカギになってきます。
2次で数学がいる人は、特に意識する必要はありません。
2次の対策がそのままセンターの勉強になってます。過去問や模試などで、形式になれることだけしておくといいでしょう。
【必読!! 新課程で受験する皆さんへ】
第3問のような、平面図形と三角比の融合は2015年度センター試験には出ません。みなさんが受ける試験は、数学Ⅰから「三角比」のみ、数学Aから選択で「平面図形」のみとなります。ですので、過去問の第3問で取れなかった人は、悲観するには及びません。 なお、期待値も出ませんが、条件付き確率は出ます。
■関連するPrinciple Piece(2016年度、新課程に合わせた内容に対応しています)■
・Principle Piece 数学Ⅰ 方程式と不等式
(第1問[1] 対応)
・Principle Piece 数学Ⅰ 2次関数
(第2問対応)
・Principle Piece 数学A 論理と集合
(第1問 [2] 対応)
・Principle Piece 数学Ⅰ 三角比
(第3問対応)
・Principle Piece 数学A 集合と場合の数
(第4問対応)
・Principle Piece 数学A 確率
(第4問対応)
・Principle Piece 数学A 整数
(新課程では出題されます!)
・Principle Piece 数学A 平面図形
(第3問対応)
Principle Piece 数学IA 原則のみ
(全問対応)
※受験ランキングに参加しています。「役に立った」という方は、クリックしていただると、すごくうれしいです^^/