センター試験 数学II・B【2010年】の難易度、傾向は?
2016/06/27
2010年に行われたセンター試験の数学IIBに関する情報についてまとめていきます。
【評価指標】
1.難易度 A(易)~E(難)
2.パターンレベル
Lv.1(習得していて当たり前)
Lv.2(習得していないと、差をつけられる可能性がある)
Lv.3(習得していなくてもしょうがない)
3.解答するまでの標準的な時間
です。これら3点から、各問題ごとにコメントしていきたいと思います。
センター試験数学Ⅱ・B(2010年)
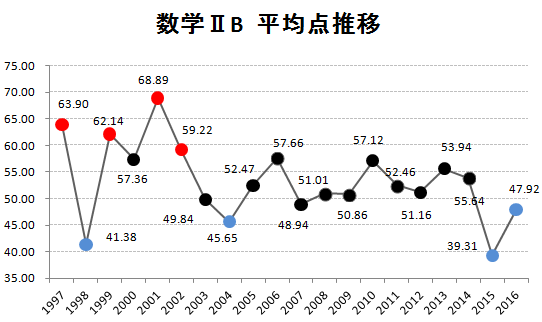
0.2010年のセンター試験IIBの平均点
まずは、1997年からの平均点推移を掲載しておきます。赤丸は平均点の高かった年ベスト4、青丸は平均点の低かった年ベスト4です。
(データを元にKATSUYAが作成 グラフの転載可)
今回の2010年は、57.12点となっています。点数から見ると例年並み、といったところでしょうか。
1.全体評価~数学IIと数Bで難易度に差がある
数Ⅱは取りやすい。数Bは多数が選択する数列(群数列)、ベクトル(空間ベクトル)でやや難。全体として例年並み。
第1問の前半の指数・対数は、人によっては頭で考えて1分で答えが出せそうなレベル。後半の三角関数は、sin18°の値を求めさせる問題で、誘導は丁寧です。
第2問の微積もラク。接線の本数と解の個数を帰着させる問題は、傍用問題集などでもよくある問題。後半の積分も、上下関係に気を付けるだけ。例年より文字が乱立せず、ラクです。
第3問はセンターでは初といわれた群数列。センター特化の対策だと対応できないでしょう。部分分数分解により和を求めさせる問題は頻出だが、群数列ができないと後半は全滅。
第4問のベクトルは平行六面体。6種を用意して3つのベクトル(p、q、r)で表す原則に従えば簡単なハズ。しかしa,b,c、s、tなど文字が乱立し、流れが見えなくなってしまった可能性があります。
■目標解答時間・・・・70~80分
穴埋めであることを利用し、多少の過程ははしょって計算をしないと、時間は足りないでしょう。日本語をなるべく書かない答案をかくつもりで。
2.各大問の難易度
第1問[1] (指数・対数、連立方程式、AB、例年比やや易、5分)
基本的な指数・対数の連立方程式です。logx、logy の対称式が得られます。数値も受験生にやさしく、暗算で最後まで解答できるような計算量しかありませんでした。
2^7=128 ぐらいは、ⅡB受験生であればおぼえておいた方がいいでしょう。
第1問[2] (三角関数、三角方程式、倍角、18°系 B、例年並み、13分)
三角方程式を解く問題です。前半は三角関数の性質を利用して角度を求めます。後半は倍角等で式変形を行い、その値を出すというもので、流れとしては良問です。
前半は文章がよくわからなくても、解くことはできます。π±θ、π/2±θ、などの三角関数は軽視されがちですが、きちんと覚えておきましょう。
後半も、誘導に従って式変形していけば、意味はわからなくても答えが出せます。に従います。3次式の因数分解では、1/2が答えの一つである(と文章に書いてある)ことを利用していくといいですね^^
第2問(接線の式、極大・極小、接線の本数、面積、B、例年並、18分)
微積分についていろいろ聞いてきますが、1つ1つは基本レベルの問題です。前半では、曲線外の点(1、0)からひいた接線の本数に関する問題。
誘導なしであれば難関大でも出題される可能性のある題材ですが、誘導があれば大したことはありません。
(Principle Piece 数学II 微分(2冊目) p.8-10)
接点もおいてくれていますし、簡単ですね^^ また、解の個数は定数分離で行きましょう。
後半は、3次関数どうしとy軸に平行な直線で囲まれる部分ですが、3次関数どうしの差をとれば2次式です。上下関係と計算ミスさえ気を付ければ、ただの作業ですね^^
第3問(群数列、部分分数分解とその和、B(新傾向)、例年並、20分)
前半は群数列に関する問題です。センターではこの年初めて出題され、少しとまどったかもしれませんが、群数列はどんなにややこしくなっても、解法パターンが変わりません。
(Principle Piece 数学B 数列 p.25)
本問ではn群の「最後」を聞いていますので、少し簡単になっています^^
600が何群にあるかですが、原則の[2]を用います。3/2×n^2-1/2×n は、ほぼ3/2×n^2 とみなせれば、n=20 と検討がつくでしょう。
前半ができれば後半はただの部分分数分解です。一番基本的な部分分数分解ですので、これはご褒美として点数いただきですね^^
第4問(空間ベクトル、内積、平面と直線の交点、B、例年並、20分)
平行六面体に関する問題です。設定から、p、q、rの3つの基本ベクトルの長さ、および内積3種(最初に聞かれています)が分かりますので、あとは基本的には何を聞かれても出せます。このように思えることが大事。落ち着いて解けます。
(Principle Piece 数学B ベクトル p.63)
XZとAHが同じベクトルであることに気づけば、EC・XZの内積も簡単に出せます。後半の直線と平面が垂直に交わる条件については、こちらの原則を用いましょう。
(Principle Piece 数学B ベクトル p.75)
本問では、[2]からアプローチです。直前でXZとは垂直であると言っていますから、XYと垂直である条件を計算すれば出ます。
後半は、[1]の原則です。式は少し違いますが、KがEC上、かつXYZ上にあることを式にし、係数比較をすればOKですね^^
※「ここはこんな風に考えて出した!」という人は、どんどんコメントください。数学は、他の人の解き方を聞くことで伸びる科目です^^
(承認制なので反映までに時間がかかります。ご了承ください)
3.センター試験II・B対策
レベル的には、教科書の章末問題レベルです。そのレベルの問題を、いかに素早く解くかがカギになってきます。計算力がものを言います。どの単元も、まんべんなく少しずつ問われますから、すべての計算を素早く計算する習慣を普段から身に付けておいてください。
2次で数学がいる人は、特に意識する必要はありません。2次の対策がそのままセンターの勉強になってます。過去問や模試などで、形式になれることだけしておくといいでしょう。
■関連するPrinciple Piece■
・Principle Piece 数学Ⅱ 三角関数
・Principle Piece 数学Ⅱ 図形と式
(第1問[1]対応)
・Principle Piece 数学Ⅱ 指数・対数関数
(第1問[2]対応)
・Principle Piece 数学Ⅱ 微分
・Principle Piece 数学Ⅱ 積分
(第2問対応)
・Principle Piece 数学B 数列
(第3問対応)