センター試験 数学I・A【2007年】の難易度、傾向は?
2016/12/18
本エントリーでは、2007年に行われたセンター試験数学IAの難易度や傾向に関する情報についてまとめています。
【評価指標】
1.難易度 A(易)~E(難)
2.パターンレベル
Lv.1(習得していて当たり前)
Lv.2(習得していないと、差をつけられる可能性がある)
Lv.3(習得していなくてもしょうがない)
3.解答するまでの標準的な時間
です。これら3点から、各問題ごとにコメントしていきたいと思います。
センター試験数学Ⅰ・A(2007年)
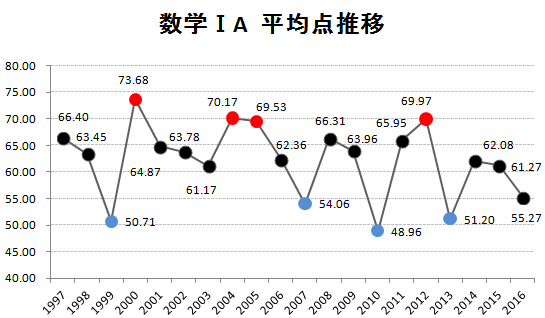
0.2007年のセンター試験数IAの平均点
まずは、1997年からの平均点推移を掲載しておきます。赤丸は平均点の高かった年ベスト4、青丸は平均点の低かった年ベスト4です。
(データを元にKATSUYAが作成 グラフの転載可)
今回の2007年は54.06点で、過去18年間でワースト4の点数となっています。
2.総評~全体的に応用的問題の割合が多く、計算量も多い~
第2問は主力の解の配置・軸分けが両方あり。加えて最後の最大値の計算がやや煩雑。第3問は面積比を多く聞かれ、方べきの定理と絡んで難。第4問の確率は類題経験で差がつき、125通りを計算できないと苦しいのに加え、全事象が多く、規則を見つける必要がある。全体としてやや難。
■目標解答時間・・・・55~65分
第3問、第4問では例年より時間がかかると思います。第2問も軸分けで、答えを出すのに最低限の計算だけをしていかないと、時間は足りない可能性もあり。
2.各大問の難易度
第1問[1] (絶対値付き方程式、√の評価、A(例年より易)、6分)
絶対付きの2次方程式です。絶対値の中身の符号で場合分けし、出た解が場合分けの範囲を満たすかどうかを吟味します。11-√17/4 と5/3 の大小はやや迷うところです。
最大解は簡単に出せますので、整数mを求めるのは問題ないでしょう。
第1問[2] (必要十分・包含関係 AB(例年比やや易)、6分)
A、B2つの集合に関する、典型的な問題です。本問は、ベン図を書けばすぐに出来たでしょう。
Aの補集合(Aバー)、Bの補集合(Bバー)などを用いて、C,D,Eを選択しを見ずに表して、一致するものを選べばOK。ドモルガンの定理を忘れずに。
C=A∩B D=Aバー∩Bバー E=Dバー ですね^^
第2問(頂点、x軸との交点、最大・最小、B(例年比やや難)、15分)
今年は主力がタッグになってきました。最初は、解の配置です。2つの交点がともに負にある範囲は、D>0、軸<0、f(0)>0です。 すぐに手が動くレベルになっておきたいですね^^
(Principle Piece 数学I 2次関数 pp.39~41)
後半は最大値の軸分け問題です。最初の3以上7以下というのは、最小値が軸のときに限定するためのものですね^^
下に凸で最大値の軸分けなら、定義域の中央(x=5)と軸(x=a-1)との大小で場合分けしましょう。
(Principle Piece 数学I 2次関数 p.27)
最小値は軸のときなので、=6をつなげて方程式を解きます。4≦a≦8 に入る方を選ぶのは簡単ですが、最大値を求める際には、3+2√3 と 6 との大小を判定しないと最後が解けませんので、結構時間かかりますね^^;
第3問 (余弦定理、外接円、内接四角形、円と直線、面積など、B(新傾向、例年比やや難)、20分)
いつも通り、三角比+平面幾何の融合問題ですが、面積比から長さを出さなければいけない問題や、最後の2連続の面積比は、普段と違った傾向で少し戸惑ったかもしれません。相似比も必要で、難易度は高め。
最初は、3辺から角度を求める手順です。余弦定理ですね^^
(Principle Piece 数学I 三角比 pp.22~23)
次は、面積比からCDとADの比を出す問題です。CD=●ADの●を求めるというのは、比を出すということです。センターでは頻出の問い方ですから、必ず頭に入れておきましょう!
普段から四角形の面積を出している人は、気づきやすいと思いますが、△ABDと△CBDは、∠Aと∠Cのsinが等しいです。従って、S1:S2はそのまま AB×AD:CB×CD となります。これを利用すると、AD:CDが出せます^^
AD=2x、CD=x とおけますので、今度は余弦定理です。こちらの原則にも注意です!
(Principle Piece 数学I 三角比 p.24)
最後は、△CDE∽△ABE に着目すると、面積比はAB^2:CD^2となります。これに気づくとかなりラクです。方べきの定理にばかり目が行きがちですが、その証明で用いる三角形の相似も、実は使えることが多いです^^
(Principle Piece 数学A 平面図形)
S1~S4まで乱立しているので、どことどこを合わせると、どこの何倍かを落ち着いて式にしましょう。
第4問(場合の数、確率、点の移動、期待値、B(例年並み)、15分)
正六角形の頂点を、サイコロの出た目に応じて移動させる設定の問題です。ルールは単純ですが、全事象が216通りあるので、規則を発見して計算をしないと数え上げるのは難しいタイプ。
最初は、3回の和が6になる目の出方を聞いています。順番も考慮しましょう。
「ウエオ」が意外と難しかったのではないでしょうか。答えは5^3=125 です。 難関中を受ける小学生だと、一瞬で解いてきます^^; 1回目、2回目、3回目において、どこに止まっていたとしても、Aに止まるための目がかならず1つだけ存在します。その目がでなければいいので、5^3となります^^
ここができないと余事象が使えず、期待値の計算にも影響しますので、差がかなりついたのではないかと思います。
回数の期待値ですが、3回は一瞬でしょう。2回止まる場合は、(6、6、6以外) (和が6の2回、6)、(6、和が6の2回) のいずれかの場合となります。
1回のときは多いので、余事象で計算しましょう。125通りが出ないと、地道になります。
※「ここはこんな風に考えて出した!」という人は、どんどんコメントください。数学は、他の人の解き方を聞くことで伸びる科目です^^
(承認制なので反映までに時間がかかります。ご了承ください)
3.センター試験対策
レベル的には、教科書の章末問題レベルです。そのレベルの問題を、いかに素早く解くかがカギになってきます。計算力がものを言います。どの単元も、まんべんなく少しずつ問われますから、すべての計算を素早く計算する習慣を普段から身に付けておいてください。
2次で数学がいる人は、特に意識する必要はありません。2次の対策がそのままセンターの勉強になってます。過去問や模試などで、形式になれることだけしておくといいでしょう。
【必読!! 新課程で受験する皆さんへ】
第3問のような、平面図形と三角比の融合は2015年度センター試験には出ません。みなさんが受ける試験は、数学Ⅰから「三角比」のみ、数学Aから選択で「平面図形」のみとなります。ですので、過去問の第3問で取れなかった人は、悲観するには及びません。 なお、期待値も出ませんが、条件付き確率は出ます。
■関連するPrinciple Piece(2016年度、新課程に合わせた内容に対応しています)■
・Principle Piece 数学Ⅰ 方程式と不等式
(第1問[1] 対応)
・Principle Piece 数学Ⅰ 2次関数
(第2問対応)
・Principle Piece 数学A 論理と集合
(第1問 [2] 対応)
・Principle Piece 数学Ⅰ 三角比
(第3問対応)
・Principle Piece 数学A 集合と場合の数
(第4問対応)
・Principle Piece 数学A 確率
(第4問対応)
・Principle Piece 数学A 整数
(新課程では出題されます!)
・Principle Piece 数学A 平面図形
(第3問対応)
Principle Piece 数学IA 原則のみ
(全問対応)
センター試験対策用の参考書については、こちらのリンクからどうぞ^^