センター試験 数学II・B【2011年】の難易度、傾向は?
2016/06/30
2011年に行われたセンター試験の数学II・BをKATSUYAが解き、その感想や各問題の難易度などをアップしていきます。
【評価指標】
1.難易度 A(易)~E(難)
2.パターンレベル
Lv.1(習得していて当たり前)
Lv.2(習得していないと、差をつけられる可能性がある)
Lv.3(習得していなくてもしょうがない)
3.解答するまでの標準的な時間
です。これら3点から、各問題ごとにコメントしていきたいと思います。
2011年センター試験数学Ⅱ・B(60分)
1.総評~前半は典型、後半は計算量が多め~
第1問の指数・対数および第2問の微分積分は毎年おなじみの典型問題でした。
しかし、第3問の数列と第4問のベクトルは少し計算量も多く、解くにベクトルは誘導形式ではなければ中堅以上の大学でも十分出題される、それなりに質の高い問題でした。特にベクトルは感覚をつかんでいないと、かなり苦労したのではないでしょうか。
制限時間60分に対し、目標回答時間は54分。
見直し含め、量としては適切ですね。
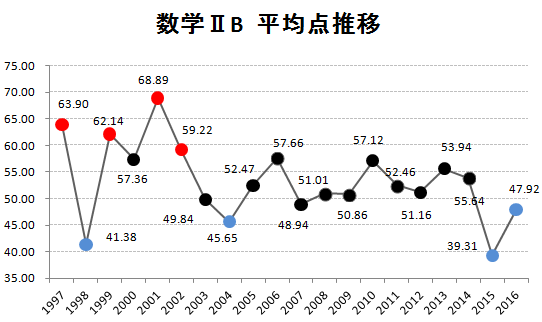
1.(1) 平均点から見た難易度
過去20年の平均点の推移から見た難易度です。センターとしては例年並みと言えます。
(※図は大学入試センター・過去問のデータを元にKATSUYAが作成)
2.各大問の難易度
第1問[1] 三角関数(AB、Lv.2、8分)
パターンとしてはLv.2ですが、過去にも出ていましたし、頻出の典型問題です。こちらの原則を用いればすぐに出来る問題です。
(Principle Piece 数学II 三角関数 p.53)※番号は見直し中なのでふっていません。
この2段階が必要な問題でしたね^^ 新高3生で出来なかった人は、チャート式などで確認しておきましょう。類題が絶対にありますから!!
最後にtの値からθの値を出すときですが、落ち着いて順番に不等式を解いてください。これが解けない人が多いです。不安なら必ず単円を書いてください。(←これは三角比のときに習得する心得です)
(Principle Piece 数学I 三角比 p.18)
※KATSUYAの解いた感想
「この手のパターンね」と見抜き、合成と t ⇒ θ の計算は落ち着いて計算して終了。ちなみに、私も単円は書きます!!
第1問[2] 対数関数(AB、Lv.1、7分)
比較的簡単な対数方程式でした。X ⇒ x の変換ミスだけ注意ですね^^ ②についてですが、、、数Ⅱ・Bの範囲では、 x + logx などの計算は変形してもうまくできません。
解は自然数と書いてありますから、代入していくしかないです。ここで時間ロスした人もいるみたいですね^^;
※KATSUYAの解いた感想
はじめの不等式で、「6X^2?なんで?係数3ちゃうの?」 とか戸惑いながら、2倍していることにすぐ気づき、あとは普通に計算して終了。 不等式②は、x=10ぐらいから 数え上げて終了。
第2問 微分積分総合 (AB、Lv.2、15分)
こちらも、例年とあまり変わらないパターンでしたね。最近円の絡んだ面積がなくて、ラクになっている印象を受けます^^
流れとしては、接線の式を求めさせる。 ⇒ 接線などで囲まれる面積を aの3次関数 で表す。⇒ 特定のaの範囲で、面積の最大値・最小値を求める。
です。微分と積分をうまく組み合わせるのに、都合がいいんでしょう(笑)
など、面積Sは裏技を使えば一瞬で出ます。センターのように穴埋めであれば威力を発揮しますね。普通に計算してもたいしたことないですが。
※KTAUSYAの解いた感想
お決まりの流れなので、単純作業に近かった。Tの面積を求めるときは計算を慎重に行い、終了。
第3問 数列(B、Lv.2、18分)
前半は、階差数列を利用して、一般項を求める問題。誘導がありますが、形に合うように、4を前に出したり( )内に入れたりと、めんどくさかったと思います。
後半は、(等差数列)×(等比数列)の和を求める問題。誘導にあるように、その和Sは、S-(公比)Sが等比数列の和として求められることを利用して計算します^^
なお、和の計算方法は、次の3通りしかありませんので、整理しておきましょう。
(Principle Piece 数学B 数列 pp.23-24)
望遠鏡型とは、部分分数分解の和の計算のように、和を並べて行くと真ん中がどんどんキャンセルされて、シュッと式が短くなるような様子を指して勝手に名づけています。
※KATSUYAが解いた感想
パターン問題ではあるものの、計算量が多い印象あり。さらに後半で(等差)×(等比)で、途中で r とか置かれて、若干混乱したものの、問題文を落ち着いて見直して計算して終了。
第4問 空間ベクトル(B、Lv.2、18分)
四角すいを題材にした、空間ベクトルの問題。しょっぱなから詰まった人もいるのでは?空間ベクトルでは、基準のベクトルは3つです。3次元だから3つだと、覚えておきましょう^^
ABCDが長方形であるということが、効いています。OD=OC+CD=OC+BA=OC+(OA-OB) (ベクトルの矢印省略)とできるので、3つのベクトルで表せます。
内分点の公式、同一平面上にあることの条件、直線上にあることの条件など、総合的に知識を運用する問題で、レベルは高かったと思われます。
※KATSUYAが解いた感想
見た瞬間、「空間かぁ」とテンションが下がり気味。 この手の問題は、分数係数の連立方程式が避けられないため、計算量覚悟で望み、終了。平面αとの交点も、誘導があったことで多少助かった印象。
3.対策~数Bの計算力に耐えられる力を~
レベル的には、教科書の章末問題レベルです。そのレベルの問題を、いかに素早く解くかがカギになってきます。
2次で数学がいる人は、特に意識する必要はありません。2次の対策がそのままセンターの勉強になってます。過去問や模試などで、形式になれることだけしておくといいでしょう。
【2016年5月28日追記】 最近は数学Bでの計算量が多めです。数列・ベクトルともに公式には文字が多く、どこに何が入るのか戸惑う人も多いです。意味をよく考えて、すぐに式が作れるように練習しておきましょう。
例:初項が5、公差が3の等差数列の第5項~第10項の和を求めよ。
等差数列の和の公式は{(初項)+(末項)}×(項数)÷2です。このように、言葉で覚えておかないと本問でミスします。
第5項(和の初項)=5+3×4=17、第10項(和の末項)=5+3×9=32、項数は10-5+1=6 よって和は(17+32)×6÷2=147(答)
■関連するPrinciple Piece■
Principle Piece 数学Ⅱ 三角関数(今年は消えましたが、一応)
(第1問[1]対応)