千葉大学全学部講評| 2023年度大学入試数学

2024/01/23

●２０２３年度大学入試数学評価を書いていきます。今回は千葉大学です。

いつもご覧いただきまして、ありがとうございます。　KATSUYAです＾＾　

２０２３年前期の大学入試数学の評価になります。

２０２３年大学入試（国公立）シリーズ。
千葉大学です。

問題の難易度（易A←→E難）と一緒に、典型パターンのレベルを３段階（基本Lv.１←→高度Lv.３）で書いておきます。
また☆は、「解くとしたらこれがいい」というオススメ問題です。

また、解答までの目標時間を、問題ごとに書きます。
※目標時間＝解き方を含め、きちんと完答するまでの標準的な時間です。

したがって、目標時間を全部足すと、試験の制限時間を越えることも、当然ありえます。
同時に、その時間の２倍考えてもまったく手がつかない場合は、ヒントや答えをみるといい、という目安にしてください。

※お知らせ

Twitter始めました　こちらもよろしくお願いいたします＾＾

Principle Pieceシリーズの販売を再開しました＾＾　こちらも予習用に適した参考書です。

YouTube開設しました。　個人的に紹介したい大学入試数学を中心に解法や発想を動画にしてみようと思います。

千葉大学
（全9問、試験時間・解答問題は学部による）

時間、解答問題が学部によりますので、総評および合格ラインについては、なしとします。ご了承ください。

１．各問の難易度

☆第１問(文系)　【図形と方程式】軌跡（B,20分、Lv.１）

座標平面上での２つの三角形の面積が等しくなる条件を求め、軌跡を答える問題。

やることは一本道で標準的ですが、２文字が絡むので計算になれていないと意外とてこずるかもです。

（１）はいいでしょう。

（２）は（１）を利用して、BP上の点Qを、p以外の文字で自分で置く必要があります。その後、三角形の面積が等しいという条件を利用しておいた文字を消去し、ｐだけにします。

（３）は（２）が出来ればほぼ勝ち確。x座標、y座標ともにpで表されているので、こちらの原則に従うだけ。

Principle Piece

媒介変数表示の軌跡 → 媒介変数を消去する

（拙著シリーズ数学Ⅱ 図形と方程式 p.52）

pの範囲も問題文で与えられているので、忘れることはないでしょう。

※KATSUYAの解答時間は13分。文系数学としてはちょうどいい。最初に持ってくると意外と差が付きそう。

第２問　【確率】さいころと得点（AB、20分、Lv.1）

サイコロの目に応じて得点が変わる問題。よく見る設定ですが、問題がただ計算が多いだけになっており、まあまあメンドウ。

（１）はいいでしょう。１点１回、２点１回です。反復試行的に考えるといいでしょう。この後の流れを見ても反復試行ですから、先に整理しておくといいですね。

Principle Piece

反復試行は１回あたりをきちんと整理する → 媒介変数を消去する

（拙著シリーズ数学A 確率 p.18）

（２）はコツコツかぞえては反復試行するしかありません。MAXで６点なので、１点か３点か５点です。何点獲得することが何回起きればいいか調査しましょう。

（３）も順番に出すしかあります。８点になる確率、７点になる確率、６点になる確率と計算し、累積で１／９を超えればそこで終了です。

※KATSUYAの解答時間は10分です。計算がメンドウなだけ。計算練習問題。

第３問(１)【２次関数】絶対値付き２次関数（AB、12分、Lv.１）

絶対値のついた放物線と直線の共有点の個数を調べる問題で、拙著シリーズにもそのまま載ってるタイプ。これは落とせませんね。

直接２つのぐらふのまま考えると、直線が斜めですので、ｐだけ移項して定数分離して視覚化です。

Principle Piece

文字定数入りの方程式の解の個数は定数分離で視覚化

（拙著シリーズ数学Ⅰ ２次関数 p.82）

ｙ＝ｐにすれば横線なので、様子をつかみやすいですね。

第３問(２)【積分法(数Ⅱ)】定積分を含む方程式（AB、10分、Lv.１）

定積分を含む方程式で、関数を決定する問題。こちらも超典型パターンなので落とせませんね。

定積分の部分はややこしく見せていますが、まずｔは積分出来て、ただの数値になります。xf(t)の部分はｘを前にだしましょう。

すると、こちらの原則を使うただの典型問題だと分かります。

Principle Piece

定積分は定数→=kとおいてk=・・・を解く

（拙著シリーズ数学Ⅰ ２次関数 p.82）

∫(-1～2)f(t)dt=kとでもおけばf(x)の形が決まりますから、それを使ってもう一回ｋと置いた式を実際に積分し、kに関する方程式を作れば、ｋは出せますね。

※ＫＡＴＳＵＹＡの解答時間合計１０分。これが第１問にすればよかったのでは？わざと？

☆第４問　【極限微分法(数Ⅲ)】（BC、25分、Lv.２）

指数関数の最大値を求め、その極限を考える問題。設定は比較的シンプルですが適度に難しく、良問だと思います。e絡みの極限の変形に慣れていないとキツイかも。

（１）は微分して＝０を解くだけ。文字が多いので慎重に。

（２）は（１）の極限を求めます。変形の仕方次第だとは思いますが、log絡みの極限なのでeの定義と派生形の基本４パターンを持ち出す原則に従いたいですね。

Principle Piece

指数・対数の極限は基本４パターンに持ち込む

（詳細は割愛。拙著シリーズ数学Ⅲ 微分法１ p.47を見てください）

1/bを指数の方に載せて、さらに逆数を取ってaを分母にするとやりやすかったかもしれません。逆数を取るかわりに指数をマイナスにするという変形が可能なので、分母が単項式になるようにするといいでしょう。

（３）は最大値の極限です。こちらもまずはM(a,b)を計算します。うまくくくっていくと、また(a/a-b)^●のような形が現れますので、逆数とって指数の符号も変えれば、ほぼ同じ式に持ち込めます。

※KATSUYAの解答時間は14分。ａ，ｂが乱立するので慎重に計算して終了。Ｍ（ａ，ｂ）の方はうまくあぶり出すのに少し時間がかかった。

第５問　【平面ベクトル】垂線の足、外心の位置ベクトル（B、25分、Lv.２）

平面ベクトルからで、垂線を下ろしたり交点出したり、外心出したりといろいろやらせてきます。問題文は長いですが、やることは大したことはありません。

（１）は平行でないことから明らかだろ、という感じですが、当たり前のことほど証明は難しいです。もし成り立つと改訂したときに、そのようなkがないということを示すことになります。使える式は3つですから、それに代入するしかないですよね。

（２）はよくある垂線の足の位置ベクトルを求める問題。基準2ベクトルはＯＡとＯＢですね。長さも内積も与えられています。基本的には何でも出せます。

Principle Piece

基準2ベクトルと「基本3量」の決定を

（拙著シリーズ数学B・C 平面ベクトル p.25）

ＨはＯＡ上です。「ＯＡ上」のように、始点Ｏが含まれている場合は実数倍だけで設定できます。

Principle Piece

交点の位置ベクトル：始点あり→実数倍で設定

（拙著シリーズ数学B・C 平面ベクトル p.39）

適当にｕ倍とでもおいて、あとは内積ゼロからｕを決定すればＯＫ。知識がある人は、正射影ベクトルでもＯＫです。直角が絡む場合は正射影ベクトルを使うとすんなり解けることが多いです。

Principle Piece

直角絡みは正射影ベクトル、内積の図形的意味も考えて見る

（拙著シリーズ数学B・C 平面ベクトル p.61）

（３）は問題文が長いですが、各線分に垂直な線引いて、その交点を求めるだけです。交点ＲはＯＡ、ＯＢで表されますから、置く文字（未知数）は「2つ」で済みます。なので、Ｒが満たすべき条件を「2つ」見つけ、式にしましょう。

（４）は（３）でt=1/2とすることに気づけば、（３）が出来ていれば瞬殺。気づかなくても、外心のベクトルを出すだけで、拙著にもそのまま載っているパターンなので、普通に求めればＯＫ。中点を設定し、垂直条件を2つ作るだけですね。

Principle Piece

外心のベクトル、ＯＡ⊥ＣＭ、ＯＢ⊥ＣＮで連立

（拙著シリーズ数学B・C 平面ベクトル p.61）

※KATSUYAの解答時間18分。(4)は気づかずもう一回計算しました＾＾；視野が狭すぎる。。。同じようなことをやらされていると思えば気づけたはずなのに。

☆第６問　【確率＋数列】確率と漸化式(サイコロと数直線)（CD,45分、Lv.３）

確率と漸化式の問題ですが、本問はかなりレベル高めです。ほとんどの人が（１）で逃げたのではないかと思います。（２）も、うまく気づけば十分でしょう。

（１）は様子をつかむための実験。ここで、いかにやみくもに計算するのではなく。状況を一般的に見れるかだと思います。実験させる問題は、得点もヒントも与えてくれています。存分に活用しましょう。

（２）から本格的な確率と漸化式。まずは3点セットを意識します。

Principle Piece

[1]n回目からn+1回目の遷移を

[2]求める部分以外の確率も文字で

[3]確率の和＝１、対称性も活かして文字を減らす

（拙著シリーズ数学B・C 数列 p.78）

ルールからして、７だけが他の座標のときに比べて特殊だと気づくこと、そして、大胆に状態を「７」と「７以外」の２つに分けられるかどうかがカギです。（２）からまともに遷移図を書こうとすると、泥沼にはまります。

2つにわけることが出来たら、簡単です。片方をpn、片方を1-pnと置きます。他の文字で置く必要もないでしょう。7に行ってしまったら永遠に７であることを忘れずに。(「袋小路の存在するパターン」と拙著シリーズでは呼んでいます。)

（３）はさらに難しい。7以外を考えるのはいいと思います。そして、２に止まることがないことも分かるでしょう。それでも状態は５つです。５つのまま頑張って漸化式を作ってもいいですが、出来れば対称性を活かしたい。そこで（１）の実験が利いてきます。

直前が１か６のときだけ１に来ることはありますが、それ以外は次に１に来ません。ですので、「5つの状態のうち、１と６だけ分けて、３～５はまとめよう」となれば状態が3つに減り、かなり遷移図か書きやすくなります。対称性を活かす原則ですね。

これで漸化式を立てます。漸化式を解くこと自体も気づけばあっけなく終わります。３～５に行く確率が係数が１／２でそろっており、何型とか関係なく簡単に求められます。そこから、１、６の確率の合計が出ます。１の確率の漸化式も、その係数がそろっているので、そのまま代入可能です。

※KATSUYAの解答時間は31分。（３）の遷移図の状態を減らすのに気づくまでがツライ。（１）の実験結果をもう一度たどってみたりしました。

☆第７問　【微積分(数III)】絶対付き定積分関数の最大値（BC,35分、Lv.２）

数式系の微積分総合問題です。絶対値付き三角関数の定積分の計算や、区間に文字が入った定積分関数の最大を求める問題。こちらも非常にシンプルですが、１題でいろいろなことが学べます。良問です。

（１）は文理共通の基本レベル。中身は合成出来る形になっています。三角関数は公式が多いです。なぜこの式の場合は合成するのか、３条件を言葉で確認しておきましょう。

Principle Piece

[1]角度が同じ　[2]種類が違う　[3]１次

（拙著シリーズ数学Ⅱ 三角関数 p.69）

今回は式の順番から見ても、cosで合成する方がいいと思います。理系の人は極方程式でも出てくる変形ですので、cosでの合成も出来るようにしておきましょう。

（２）は０～２π までの積分ですが、合成角は不明なので、このままでは積分しにくいです。グラフと区間を平行移動します。この関数は周期関数ですから、その後、区間を０～２πにもどすといいでしょう。そのことをきちんと証明しないと減点を食らうかどうかは分かりませんが、それは残り時間に応じて決めましょう。

Principle Piece

周期関数の積分 → 平行移動による置換も有効

（拙著シリ「ーズ数学Ⅲ 積分法(数式編) p.69）

（３）も、周期が２πであることを利用すると、平行移動して合成角の影響を排除したほうがいいでしょう。場合分けは多く見えますが、明らかにｔ～ｔ＋π/3がπ/６～１１π／６内にあるときに最大はありそうです。そうでない区間では最大にならないことを述べたうえで(S台さんの解答がスッキリしていていいと思います)、その区間だけ計算すればいいでしょう。

計算結果の式は微分するまでもなく、和積を用いるか、一度展開して合成をすれば簡単に最大値は分かります。

※KATSUYAの解答時間は25分。平行移動の知識なども確認できるいい問題。(３)も典型パターンやけど、+αの一工夫で場合分け減らせる。

☆第８問【複素数平面】方程式を満たす複素数の個数（BＣ,35分、Lv.2）

複素数平面の問題です。z^n＝ｉとなるｚの個数を吟味する問題。だんだん難しくなるので、うまく差が付きそうな問題です。やることはあまり変わりませんが。

（１）は極形式などにして求めるだけです。教科書レベル。偏角は２πずれ注意。

Principle Piece

極形式での「＝」 → 偏角は＋２ｋπを忘れずに

（拙著シリ「ーズ数学B・C 複素数平面 p.22）

（２）も（１）と同じです、解は１００個あります。実部と虚部で条件が与えられていますが、偏角の範囲に簡単に直せます。その偏角も範囲に入っているものを数えるだけですね。

（３）もやることは同じ。ほぼ同じことを行いますが、偏角の範囲は０～２πにすると該当箇所が途切れるので、ーπ～πにしておくと、範囲が途切れずに数えやすいと思います。この辺りは状況に応じて臨機応変に変えたいですね。

範囲に入る条件を作っていくと、ｎを６で割った余りで分ければうまく来そうだと分かりますので、あとはコツコツわけていくだけ。

※KATSUYAの解答時間は22分。（３）でーπ～πの範囲に変えたほうがいいと気づけるかどうかで、答えやすさは大きく変わりそう。

☆第９問　【微分法】抽象的関数が最大値を持つことの証明など（C、30分、Lv.2）

関数に関する条件だけから、関数が最大値を持つことや、その最大値について考察する問題。関数が具体的に与えられていないので受験生は苦手そうですが、千葉大は結構こういう問題見ます。(後半の医学部、理学部数学科用問題などで)

（１）は微分して具体的に与えられているので微分して増減表を書けば簡単にわかります。

（２）もまだ出来ると思います。一度微分して＝０とするとf'(x)=ｔとなりますが、条件からこのようなxは１つだけあり(ｘ＝●とします)、その前後で導関数は正から負になるので、極大かつ最大ですね。

（３）は難易度が上がります。st-g(t)を(２)を利用して書き換えると、f'(●)のような形が出ます。ここで、f'(x)は連続とは書いてありますが、微分可能とは限らないので、この式を微分してしまうと大幅減点になります。

ただ、(してもいいなら)微分することで、●＝ｓのときに最大値をとることが予想が付きますので、そうでないときにこの関数がf(s)より小さいことを示します。

不等式の証明なので差を取りますが、その式が平均値の定理が使える形に帰着出来ると気づかないとここで詰まるでしょう。s-●、f(s)-f(●)の形が両方あ
ることなどから着想を得たいですが、難しいでしょう。

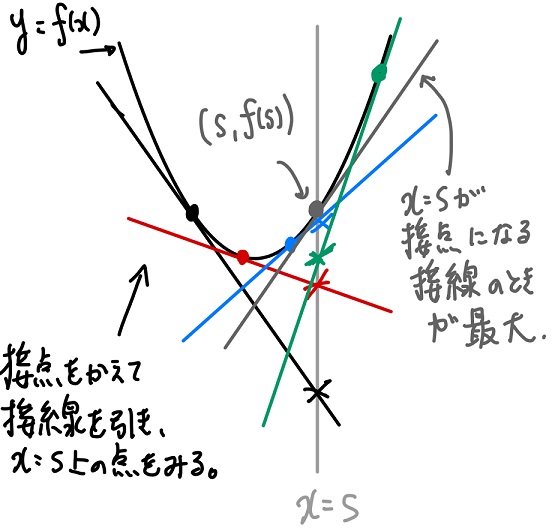
イメージとしては、st-g(t)はy=f(x)上のx=●における接線の式に似ています。また、(厳密にはダメですが)性質からf''(x)>0に類似した関数ですから、下に凸の関数とみなせば、接線は接点を除けば関数の下側を通ります。

x=●における接線を考えて、接線上のｘ＝ｓの点のy座標を見るなら、それが最大になるのはｘ＝ｓがそもそも接点になるときで、最大値はｙ座標f(s)ってことですよね。

※KATSUYAの解答時間は18分。具体的な計算が少ない分、思いついたら楽な問題。思いつかないと(２)どまりかな。千葉大、最後の方にこういうの出すから油断できない。

２．対策～癖のある表現、全調査タイプ、定数入りの計算に対する耐性を～

千葉大の問題は標準的な問題が多いですが、後半になると癖が強く、対策してきても数学的センスがないと、効果が出せないようなタイプの問題が出ます。また、全調査をすることを厭わない忍耐や、定数が入ってもいつもどおりの解法が遂行出来ることが必須となります。

青チャートなどで手法を身につけたら早めに入試演習に入りましょう。表現をひねってくる問題も多いので、国立系の入試問題集（Canpassなど）がいいです。その際、複数の解き方を試みて、いろんな視点から問題を眺められるようにしておくといいです。（式で見るのか、図形で見るのかなど）過去問はなるべく多く確保しておきましょう。

量をこなす演習：じっくり演習＝８：２でOK。　医学部や理学部志望の方は、夏あたりから７：３、６：４に切り替えていきましょう。