早稲田大学教育学部数学講評| 2024年大学入試数学

2024/02/21 2024/02/22

※動画、画像が読み込まれないときがあります。その場合、画像なら余白を、動画は文字リンクをクリックしてください。

●２０２４年度大学入試数学評価を書いていきます。今回早稲田大学(教育学部)です。

２０２４年大学入試（私大）シリーズ。
早稲田大学(教育学部：理系)です。

問題の難易度（易A←→E難）と一緒に、典型パターンのレベルを３段階（基本Lv.１←→高度Lv.３）で書いておきます。
また☆は、「解くとしたらこれがいい」というオススメ問題です。
また、解答までの目標時間を、問題ごとに書きます。
※目標時間＝解き方を含め、きちんと完答するまでの標準的な時間です。

したがって、目標時間を全部足すと、試験の制限時間を越えることも、当然ありえます。
同時に、その時間の２倍考えてもまったく手がつかない場合は、ヒントや答えをみるといい、という目安にしてください。

★お知らせ★

Principle Pieceシリーズ販売中です＾＾　原則習得のための参考書です。

YouTubeチャンネルです　個人的に紹介したい大学入試数学を中心に解法や発想を紹介していこうと思います。

Twitter　こちらもよろしくお願いいたします＾＾

早稲田大学（教育学部：理系）
（試験時間120分、4問、記述式、一部答えのみ）

１．全体総評～うまく選べば点数は取れそう～

昨年比でほぼ変化なしか、やや易化という感じです。難しい問題もありますが、方針がすぐ立つ問題もありますので、そこで稼ぐことが出来ればそれなりに点数に結びつくと思われます。いつも通り、第１問にまともにやると時間を食いそうな問題がチラホラ。答えだけですから、多少のカンも必要です。

試験時間120分に対し、標準回答時間は169分【137分】（←答えのみを考慮）

2023年：182分【153分】

2022年：164分【144分】

2021年：137分【124分】

2020年：152分【128分】

2019年：148分【134分】

2018年：174分【142分】

2017年：152分【131分】

2016年：128分【117分】

2015年：127分【107分】（答えのみを考慮）

2014年：165分

２．合格ライン～第２問がある意味合否を分ける～

第１問は(1)(4)は確実に取りたい。(2)(3)はまともに論述してられないので、カンで書くのがいいでしょう。ここのカンが当たるかどうかでちょっと差はつくでしょう。(2)の方は中受組だと思いかびやすい形があるかも。

第２問について。合否を分ける問題には2種類あります。1つは単純に解けるか解けないかが合否を左右する。もう一つは、手を付けてしまったがゆえに時間を浪費し、合格が遠のく。本問は後者のパターン。これ見て、瞬時に後回しにした人は、後ろに手が付いたので点数が稼げたでしょう。本問は手をつけるべき問題ではありません。数学が得意な人、数学で突破しようとしている人ほどこういうのに手をつけがち。(もちろん解けるならいいですけど)

第３問、第４問は時間さえあれば計算が多いだけなので取れる。特に第4問は、第2問を後回しにしたかどうかで出来が分かれるでしょう。

時間があるうちに、第１問（１）（４）、第３、４問をしっかり確保。第1問(2)(3)はある程度考えてカンでどちらかでも当てたい。第2問は残り時間で書けることを書き、考えたことをアピールするぐらいが関の山といった感じでしょう。60%強ぐらいあればいいですかね。

３．各問の難易度

☆第１問(1)【整数】2進法の循環小数（AB,9分【6分】、Lv.2）

4/9を2進法の循環小数に直す問題。結構盲点な問題で、一定数は出来ないと思いますので、適度な難易度だと思います。

小数だろうが分数だろうがやり方は同じ。２倍して１未満ならその位は０、１を取り出せらたら１を書き、の残りをまた2倍して同じことを繰り返します。4/9に戻ってきたらＯＫ。

4/9×２＝8/9＜１　→小数第一位０

8/9×２＝1と7/9　→小数第２位１　(←数値で帯分数表記が役に立つ唯一の例でしょうかね＾＾；)

7/9×２＝1と5/9　→小数第３位１

・・・みたいな感じで繰り返します。

慣れていると、分母が９なら循環節が６やろうなぁと予想がつくと速いです。(2^n-1が9の倍数になる初めてのnが6なので)

第１問(2)【空間図形？】空間上の格子点だけで構成される最小正六角形（B,15分【8分】、Lv.2）

全てが格子点だけで出来る空間上の正六角形の中で、最小のものの1辺を求める問題。記述だと書きにくいので、試験では「そこそこやって、あとエイヤー」するパターンですね。

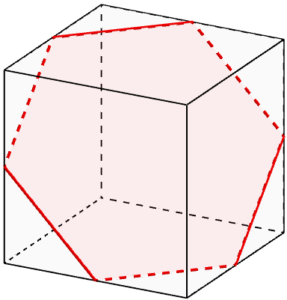
1辺１だとさすがに無理なことは分かると思います。斜めにしようと思うと、どうしても１より大きい長さが必要。次は最低でも√２ですが、これは再現可能。中受組は真っ先にこの形が思い浮かぶのではと思います。(なぜなら、算数も教えている私がこれを真っ先にイメージしたから＾＾;)

立方体の切断面ですね。立方体の1辺の長さを２にすれば、頂点は全部格子点におけます。これで長さ√２になります。

第１問(3)【平面図形】対称軸の存在と多角形（BC,25分【10分】、Lv.2）

こちらも、「そこそこやってあとエイヤー」のタイプです。まともに記述しようと思ったらこれだけで、第3問と同じぐらい時間消費する可能性あります。

対称性の高い多角形の方が対称軸は多いし均等だろうという予想を立てれば、辺の長さがなるべく少ないのは正多角形だろうと予想し、純に書いていけば、30度間隔に出来るのは正六角形だと予想が付きますので、「６ってと書いちゃえ！」で逃げるのが試験では正解のムーブでしょう。私もこれで逃げています。

ちゃんと証明するのはかなりメンドウですので、予備校さんの解答なりを見て下さい。

☆第１問(4)【図形と方程式＋積分】存在領域の面積（B,20分【13分】、Lv.1）

対称式で表された座標の存在領域の面積です。ｘ、ｙの範囲にひねりがあるので、こちらも適度な難易度で良問かと思います。

対称式絡みの領域では、対称式を主役にしますが、暗黙の条件に注意ですね。

Principle Piece

対称式絡みの領域では「暗黙の実数解条件」に注意。

（詳細は拙著シリーズ数学II 図形と方程式 p.96）

明文化されていない実数解条件です。和と積から作れる2次方程式の実数解条件が暗黙の条件として入ってきます。

あとはその方程式の解の条件に帰着しますが、どちらも０≦ｔ≦１にあればOKです。そのうち大きくない方をｘとすれば条件は満たされます。x，yの大小はあまり影響がないわけですね。

あるいはｘ＋ｙ＝ｋとして固定してもOKです。そのときのxy＝x(ｋ-x)ですので、取りうる値の範囲を求めます。この場合、ｋ＝１を境にしてｘの定義域が変わることに気を付けます。

後者は結構汎用性が高い(条件式が対称でなくても通用することが多い)ので、どちらの方法でも解けるようになっておきたいですね。学びの多い良問だお供居ます。

面積は放物線と2接線のタイプなので、答えだけなら12分の3乗公式でもOK。まともにやってもあんまり変わりませんが。

※KATSUYAの解答時間は順に2:49、1:20、1:36、4:41。また予想でエイヤー問題来た。教育の第1問、こういうのホンマ好きよな。こちとら時間測ってやってますんで、(2)は立方体の切断面で√２、さらに(3)も6角形でさくっと逃げますよ、と。(4)はｘ＋ｙ＝Xで固定する方法にしましたが、両方０～１でもたいしたことないかな。通過領域の一部みたいな図も出てきたのでまああっていると判断。(2)は合ってるはず。(3)は時間が余ったらじっくり考えればいい(余りましたが、結局考えませんでした)。

第２問【複素数平面】条件を満たす集合の性質（CD、50分、Lv.MAX）

3つの複素数に関して、ｎ乗し続けた時の集合はみんな一致するときに、どんな集合かを考察する問題。文句なし本セット最難問、そしてほぼ捨て問確定の問題です。変に手をつけて時間を浪費した人の方が、解けるはずの第３問、第4問も落とすという結果になります。そういう意味で、合否を分ける問題。

(1)は、z1は何乗かすれば1になることが言えれば、ほぼ同時に示せますが、これもなかなか難しいですね。z1のk乗はz1(の1乗)に、逆にz2のｍ乗がz1(の1乗)に等しくなる。そんなｋ、ｍ(2以上)が、条件から必ずあるはずです。

これを合わせることでz1のkm乗がz1に戻りますので、うまく示せそうですね。

(2)は（１）から、ｚ１は１の何乗根かで表されるもの(１以外)であることが分かります。また、要素の中にｚ１、ｚ２、ｚ３および１が入るはずですので、最低４つです。あとはここから探していけばいいでしょう。4乗根では１以外の３つでは条件は満たされず、5乗根であれば満たされますね。５という数字が素数であることもポイントになっています。

言われてみればどうってことないですが、高度な知識があることが解法を思いつくための必要条件となっているような問題のため、受験生が思いつくのはかなり困難です。

～本問に対して思うこと(ちょっとぼやき入ります)～

個人的にはこういう問題はあまり好きではありません。大学数学、しかも理系でも全員ではなく、一部の人が大学後半で学習するであろう内容の「群論」が背景になっていると思われます。試験を突破する上で大事なことは、「このレベルの問題をきちんと完答出来る実力」よりも、「危険な香りを感じてこんな問題は後回しに出来る判断力」を身につけることです。

※大学で数学科とかを出ていて、数学だけには精通している(と思っている)、いわゆる「数学バ●」の類から批判が来そうですので、「試験を突破すうえで」ということを繰り返しておきます。受験生は数学だけ1日中やってりゃいーってわけではないので。

こういう問題が出題されると、

「うちの塾では、こういった問題にも対応できる力を身につけさせていますよ！！」

みたいなビジネスをする輩が増えるんですよね。そして高度なことを教えるという名目で、だいたい高額。こんな問題、癖強めの私大か医科大あたりが、たま～に出すか出さないかぐらいです。こんな問題よりも後の第3問、第4問を確実に解ける力を身に着ける方が、受験数学においては数倍大事です。受験数学の指導としては、はっきりいって無価値に近いうたい文句に騙されないようにしましょう。この問題に対応できる力は、大学に入ってから身につければOKです。

そういう意味でも、大学数学ががっつり背景として見えるような問題はあまり出題しないで欲しいと思います。情弱ビジネスを展開し、それにだまされる高校生が増えますんで。

～ぼやきここまで～

※KATSUYAの解答時間は24:20です。昨年の京大理系の6番然り。高校数学を超えるであろう知識・背景の有無で有利、不利が大幅に変化する(検算に使えるなど、僅かなら全然OK)ものは個人的には出さないで欲しい。