九州大学文系数学講評| 2023年度大学入試数学

2023/03/05 2024/01/23

※動画、画像が読み込まれないときがあります。その場合、画像なら余白を、動画は文字リンクをクリックしてください。

●２０２３年度大学入試数学評価を書いていきます。今回は九州大学(文系)です。

いつもご覧いただきまして、ありがとうございます。　KATSUYAです＾＾いよいよ、２次試験シーズンがやってきました。すでにお馴染みになってきたかもしれませんが、やっていきます。
２０２３年　大学入試数学の評価を書いていきます。

２０２３年大学入試（国公立）シリーズ。
九州大学(文系)です。

問題の難易度（易A←→E難）と一緒に、典型パターンのレベルを３段階（基本Lv.１←→高度Lv.３）で書いておきます。
また☆は、「解くとしたらこれがいい」というオススメ問題です。

また、解答までの目標時間を、問題ごとに書きます。
※目標時間＝解き方を含め、きちんと完答するまでの標準的な時間です。

したがって、目標時間を全部足すと、試験の制限時間を越えることも、当然ありえます。

同時に、その時間の２倍考えてもまったく手がつかない場合は、ヒントや答えをみるといい、という目安にしてください。

★お知らせ★

Principle Pieceシリーズの販売を再開しました＾＾　原則習得のための参考書です。

YouTube開設しました。　個人的に紹介したい大学入試数学を中心に解法や発想を紹介していこうと思います。

Twitter始めました　こちらもよろしくお願いいたします＾＾

九州大学（文系）
（試験時間120分、4問、記述式）

１．全体総評～実質前半3問勝負か～

昨年比で変化なしです。第1問~第3問は標準的な問題で、第4問の確率と漸化式だけレベルが違うという感じでした。最初の3問でしっかりとれるかどうかのセットという感じです。

分野的には、グラフ主体の微積が2問、あとはベクトル、確率と漸化式です。今年は確率が復活し、あとは微積と数Bという感じでした。

試験時間120分に対し、標準回答時間は105分。

2022年：105分

2021年：90分

2020年：95分

2019年：88分

2018年：75分

2017年：85分

2016年：115分

2015年：85分

2014年：110分

2013年：100分

2012年：130分

2011年：105分

2010年：120分

２．合格ライン

第１問は絶対付き2次関数と面積。標準的だが、意外とキー問題かと。S2をまともに出そうとするとキツイ。

第２問は微分法と少し図形的な要素が入っているが、順番に出せば解けるはず。

第３問のベクトルは文理共通問題だが、文系はかなり簡単に設定されている。(3)はキー問題。

第４問の確率と漸化式は(1)(3)はいける。(2)もなんとか取りたい。(4)は無視でOK。

第１問~第３問を全て完答出来れば勝ち確。最低2題は欲しい。第4問(4)以外と合わせてラインとしては６０％~６５ぐらいでしょうか。

３．各問の難易度

☆第１問【2次関数＋面積】2つの部分の面積が等しくなる条件（B,20分、Lv.２）

絶対値付き2次関数と直線で囲まれる部分の面積で、題材的には昨年とかなり似ています。意外と問題集にありそうでない問題。

S1やS2、特にS2をまともに出そうとするとかなりキツイです。面積が等しいので、共通部分を加えて出しやすくします。絶対値付き関数と直線で囲まれた部分は、6分の公式の足し引きで楽に出せることが多いです。今回もこの原則に従いましょう。

Principle Piece

絶対値付き放物線と直線→「6分の公式」の足し引きで

（詳細は拙著シリーズ数学II 積分法 p.60 参照）

今回はS1の真下と、さらにー３~３の部分をひっくり返した部分も加えましょう。これで、どちらもほぼ6分の公式で出せます。

答えの形からしても、6分公式の足し引きで出さないとａに関する方程式を解くのはキツイと思います。

※KATSUYAの解答時間は7:53。共通部分付け加えることに気づけば勝ち確の問題。

☆第２問【微分法+図形】3次関数の接線と直線のなす角など（B,25分、Lv.2）

3次関数の接線と、ｙ＝－ｘ(変曲点における接線)とのなす角に関する考察です。誘導のやり方は正直遠回りだと思いますが、素直に従えばそこまで大変ではない問題かと。

（１）は接線を出してｙ＝－ｘと連立するだけです。

（２）は2直線のなす角ですので、tanの加法定理を用います。2直線の傾きをtanと結びつけましょう。

Principle Piece

直線の傾きとなす角はtanで結びつく

（詳細は拙著シリーズ数学II 三角関数 p.46 参照）

Principle Piece

2直線のなす角は tan の加法定理

（詳細は拙著シリーズ数学II 三角関数 p.47 参照）

今回はなす角が90°になることがあるので注意が必要。90°でないときと分けてtanの計算をし、最後にsin^2θの式まで出したときに、θ=90°のときも成り立つことを確認しましょう。

（３）は(2)を利用する必要があるのか疑問ですが、OPは外接円の半径ですから、OP/OA＝1/2sinθです。なのでθ=90°のときが最小値になるのは当然で、かつ(2)で90°になるときがあることをわざわざ確認していますので、最小値は1/2ですし、そのときの接線の傾きはｙ＝－ｘと直交して１ですから、ｔの値も出ます。

(2)の複雑な式をわざわざ使う必要はない気がします。おそらく(1/t)の2次関数とみて平方完成させたいのだと思います。

※KATSUYAの解答時間13:51。(2)いる？余計メンドクサイんやけど＾＾；　いきなり(3)だと解けない人多いと踏んで、問題数増やしたかな。

第３問【平面ベクトル】2つのベクトルが平行である条件（B、25分、Lv.2）

4次方程式を題材に、虚数解や整数解を持つ条件を求める問題。（２）はそれまでの誘導以外にも考えることが多く、少し難しめです。

（１）は、イメージとしてはａ：ｂ＝ｃ：ｄということなので当たり前ですが、成分のうち片方が０になることがあるのでそのときは別で議論するので注意。必要十分条件なので、両方の向きを調べることに注意。

あるいは、平行であるときはなす角が0°または180°なので、「内積＝±絶対値の積」から2乗して変形していくのもありです。コーシー・シュワルツの不等式のような式が出てきます。

（２）はｖ，ｗの成分を文字でおいて、コツコツ成分入れて連立計算するだけです。

（３）はｑの成分を文字でおいてｒ、ｓを出してもいいですが、それをｑ、ｖ、ｗに戻せるかどうかです。うまく内積と気づけば戻せます。

あるいは、（２）を利用すれば文字で置くことなく、瞬殺できます。例えば両辺にｖをかければ、ｖやｗは(2)の性質を満たすので、ｒ＝ｑ・ｖだけが残りますので、そのままこれが答えです。

※ＫＡＴＳＵＹＡの解答時間は15:54です。（3）は少し考えて、(2)の利用に気づく。これは気づかないと意外と詰まるかも。成分で置くという発想にはならなさそう。

☆第４問【確率＋数列+複素数】確率と漸化式、サイコロの目と複素数（C、40分、Lv.2）

最後は確率と漸化式からです。サイコロの目に応じてωをかけたり共役をとったりしますが、設定がまあまあメンドウなので、遷移を書くのにかなり時間を持ってかれますし、問題自体もまあまあ後半は難しいです。特に(4)は理系で出てもキツく、捨て問でしょう。

（１）は実際にωを出すなり、共役との積が１＝ω^3から導くなりすればＯＫ。

（２）は1回目の確率と漸化式。確率と漸化式では、ｎ回目からn+1回目を詳しく見ます。

ｎ+1回目に０になるのは、ｎ回目に０でないときから来ますので、求めたい確率以外の部分も考えます。今回は「０」か「０でない」かの２つの状態だけなので、ｐｎと１－ｐｎで置けます。状態が2つの時は楽です。

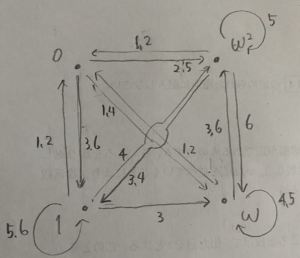
（３）は(4)への布石になりますが、遷移の状態が多い上に、どの状態からどの状態にも行けるので、整理がかなり大変。私はこんな感じで、どの目が出ると数値がどう変わるかを整理しました。ルールも多いので、計算ミスをしないように慎重にやる必要があり、この図を書くのに時間をかなり持っていかれるでしょう。

この図さえかければ、あとは慎重に調べます。例えばｚ３＝１となるには、０からは3,6の目、１は5,6の目、ωからはなし、w^2からは3,4の目が出ればOKでとすぐにわかります。遷移図の威力が分かる例だと思います。

計算していくと全て同じ結果になることが分かります。これをもとに、０以外の１、ω、ω^2になる確率はずっと等しいのではないかと予想がつきます。これが(4)で使えます。

(4)はまず予想を証明します。ｎに関する証明で、結果が予想できるなら帰納法と相性がいいですね。(2)同様、求めたいところ以外の確率も必要。まだ等しいかどうかわからないので、全状態の確率を設定しておきます。それで漸化式を作れば、１、ω、ω^2ですべて等しいことが分かりますので、(2)を利用して１から引いて３で割ればOKです。

これは難しめの確率と漸化式でしたが、０だけが他に比べて仲間外れなので先に０だけが出せること、対称性の予想や遷移図を書く練習になりますし、演習価値の高い問題ですね。

※KATSUYAの解答時間は27:14です。確率と漸化式は好きなのでこの手の問題は苦ではないですが、今回は遷移図が繁雑で慎重にやりました。問題としては良問。いつか動画で紹介したいですね。