早稲田大学 人間科学部(理系) 数学 講評| 2023年大学入試数学
2024/01/05
※動画、画像が読み込まれないときがあります。その場合、画像なら余白を、動画は文字リンクをクリックしてください。
●2023年度大学入試数学評価を書いていきます。今回は早稲田大学(人間科学部B:理系)です。
2023年大学入試(私大)シリーズ。
早稲田大学(人間科学部B:理系)です。
問題の難易度(易A←→E難)と一緒に、典型パターンのレベルを3段階(基本Lv.1←→高度Lv.3)で書いておきます。
また☆は、「解くとしたらこれがいい」というオススメ問題です。
また、解答までの目標時間を、問題ごとに書きます。
※目標時間=解き方を含め、きちんと完答するまでの標準的な時間です。
したがって、目標時間を全部足すと、試験の制限時間を越えることも、当然ありえます。
同時に、その時間の2倍考えてもまったく手がつかない場合は、ヒントや答えをみるといい、という目安にしてください。
★お知らせ★
Principle Pieceシリーズ販売中です^^ 原則習得のための参考書です。
YouTubeチャンネルです 個人的に紹介したい大学入試数学を中心に解法や発想を紹介していこうと思います。
Twitter こちらもよろしくお願いいたします^^
早稲田大学(人間科学部B:理系)
(試験時間60分、5問、穴埋め型)
1.全体総評~やや軽めに~
2020年~2022年は以降の理系専用問題を中心に計算量の多いセットで、今年は共通部分で軽い問題があることで少し軽くなりました。
理系専用問題からは5年連続出題の複素数平面が姿を消し、両方とも微積分となりました。
試験時間60分に対し、標準回答時間は99分【分】(←穴埋め考慮)
2022年:110分【74分】(←穴埋め考慮)
2021年:113分【78分】(←穴埋め考慮)
2020年:101分【68分】(←穴埋め考慮)
2019年:89分【57分】
2018年:63分【42分】
2017年:91分【56分】
2016年:82分【51分】
2015年:100分【59分】
2.合格ライン
第1問~第3問は文系と同様。理系なら第3問は計算を合わせたい。
第4問は意外とキー問題か。やることは明確で単純だが、計算が合うかどうか。
第5問は前半はなんとか。後半はきついか。制限時間もあり、キツイかも。
第4問までしっかりとれていれば出来なくてもという感じ。最後は発想も必要。
文理共通問題で出来る限り落とさずにとれば、第1問~第4問で3完していれば安心。あとは時間の限りつまみぐいでいいでしょう。
※点数標準化による得点調整があるため、あくまで目安です。
3.各問の難易度
第1問[共]、第2問[共] 第3問[共]
文系と共通なので、割愛いたします。詳しくは、1つ前のエントリーをご覧下さい。
第4問[理]・・・【微積分総合】極値、回転体の体積(AB、18分【12分】、Lv.2)
微積分総合問題で、回転体の体積です。減衰曲線が題材で、面積の級数などを出す問題としてよくあるパターン。計算が比較的メンドウなのもお決まり。今回は回転体なので、まあまあ繁雑です。2023年は関西学院大理系でも出題されています。
極値の値は微分すれば出ます。回転体の体積は2乗した式を積分しますが、2乗した式はe^2xsin^2xとなりますので、積分はそれなりに骨が折れます。順番に式変形しましょう。
まず、三角関数の積分は次数を1次に下げます。半角、もしくは積→和の公式です。
次数を下げると、e^2xcos2xが出てきます。このタイプの積分は、相方を持ち出して両方微分すると比較的ラクでしたね。これで不定積分を求めてから一気に代入するといいでしょう。答えだけなので、代入計算は慎重に。
※KATSUYAの解答時間は5:07です。ただの計算問題ですね。
☆第5問[理]・・・【空間ベクトルなど】軌跡、体積など(BC、30分【20分】、Lv.3)
最後は、第3問に続いて空間ベクトル+積分からです。空間ベクトルが5題中2題です。球の接線とxy平面との交点の軌跡を求めたり、光が当たる部分の体積を求めたりする問題です。前半は難関大であればちょくちょく見かけますが、後半は難しめ。
前半は誘導に従いますが、最初の「テ」が出来ないと意外とキツイか。内積は、正射影ベクトルとの積です。円、球の接線絡みの内積は、図形的意味も考えると簡単に答えられることが多いです。最初が出れば、Q(x,y,0)とおいて成分を入れて計算するだけです。
このタイプは普段は違う解き方でやりますが、この方法もかなり明解でいいですね。
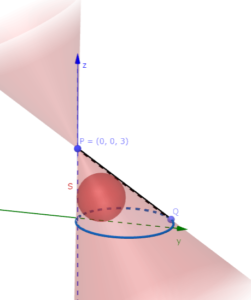
後半は少し難しめ。図が斜めになっているので分かりにくいですが、直円錐の中に球が入っているだけですので、直円錐から球の一部を引けば出せます。yz平面で考えると平面の世界に出来ます。球、円絡みは中心を通る平面を考えるのが原則です。
(詳細は拙著シリーズ 数学I 三角比 p.64 参照)
球の方は座標設定して回転体の体積として出せます。
※図形をコンピュータに書いてもらうと、球面S、P、Qはこんな感じになります。
※KATSUYAの解答時間は10:59です。今年はまあまあ本格的な求積でした。
4.対策
IAIIBは、文系と同様の対策でOK。内容的には、1歩進んだ典型パターンが多めです。青チャートのコンパス3~5ぐらいが解けるようにしておけば大丈夫でしょう。制限時間との勝負になります。穴埋めならではの飛ばし方も練習しましょう。
理系の第4問、第5問は微積(積分寄り)と、新課程の複素数平面が多い印象です。(今のところ5年連続)。穴埋めなので最後の1行でも計算ミスすると0点ですから、正確に計算できるように訓練しておきましょう。
量をこなす演習:じっくり演習=10:0でOK。60分でじっくり考えないといけない問題は、捨てて問題ないでしょう。
以上です^^
■関連する拙著『Principle Pieceシリーズ』(リニューアル版!)■
数学I Chapter4~三角比~ (第5問)
数学A Chapter1~集合と場合の数~ (第1問(1))
数学A Chapter2~確率~ (第1問(1))
数学II Chapter2~複素数と方程式~ (第1問(2))
数学II Chapter2~指数関数・対数関数~ (第1問(3)、第2問)
数学B・C Chapter3B~空間ベクトル~ (第3問)
数学III Chapter4~微分法2~ (第4問)
数学III Chapter6~積分法(グラフ編)~ (第4,5問)
すでに原則系の参考書を持っている方にはこちらがおススメ!!
※2023年6月末時点で販売中のもののみ記載しています。最新販売情報はこちらからどうぞ^^
>> 2010年度
>> 2012年度
>> 2013年度
>> 2014年度
>> 2015年度
>> 2016年度
>> 2017年度
>> 2018年度
>> 2019年度
>> 2020年度
>> 2021年度
>> 2022年度
★お知らせ★
Principle Pieceシリーズ販売中です^^ 原則習得のための参考書です。
YouTubeチャンネルです 個人的に紹介したい大学入試数学を中心に解法や発想を紹介していこうと思います。
Twitter こちらもよろしくお願いいたします^^