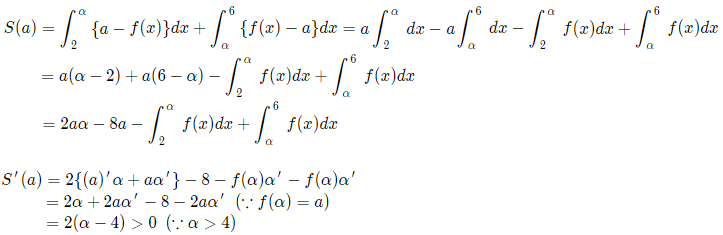北海道大学 理系 講評 | 2022年度大学入試数学
2022/12/13
●2022年度大学入試数学評価を書いていきます。今回は北海道大学(理系)です。
いつもご覧いただきまして、ありがとうございます。 KATSUYAです^^いよいよ、2次試験シーズンがやってきました。すでにお馴染みになってきたかもしれませんが、やっていきます。
2022年 大学入試数学の評価を書いていきます。
2022年大学入試(国公立)シリーズ。
北海道大学(理系)です。
問題の難易度(易A←→E難)と一緒に、典型パターンのレベルを3段階(基本Lv.1←→高度Lv.3)で書いておきます。
また☆は、「解くとしたらこれがいい」というオススメ問題です。
また、解答までの目標時間を、問題ごとに書きます。
※目標時間=解き方を含め、きちんと完答するまでの標準的な時間です。
したがって、目標時間を全部足すと、試験の制限時間を越えることも、当然ありえます。
同時に、その時間の2倍考えてもまったく手がつかない場合は、ヒントや答えをみるといい、という目安にしてください。
★お知らせ★
過去にTOP10を独占した数学の問題集『Principle Piece』シリーズの販売再開!
こちらも、原則習得のための参考書です。
YouTube開設しました。 個人的に紹介したい大学入試数学を中心に解法や発想を動画にしてみようと思います。
Twitter始めました こちらもよろしくお願いいたします^^
北海道大学(理系)
(試験時間120分、5問、記述式)
1.全体総評~バランス崩壊レベルの大幅難化~
大幅に難化し、講評をして以来最難レベルのセットでした。また、前半の3問がかなり難易度が高く、後半の2問が手が付けやすいという配置が、受験生を精神的に追い詰める配置です。難易度の差が前半と後半で大きく、北大にしてはめずらしく少しバランスが崩れているセットです。東大・京大・東工大あたりを志望している人もぜひ、といいたいセット。
北大理系は良問のセットなので、普段は☆マークもたくさんつくのですが、今年は少なめになっています。
第1問飛ばし・・・第2問にとりかかってまた苦戦。第3問も苦戦・・・で穏やかな第4,5問にいくときにはMPを消費している(精神的にイライラ、疲弊している)状態という受験生がたくさんいたことでしょう。
数学力ではなく、精神力を測りに来ている?
試験時間120分に対し、標準回答時間は155分。ただし最初の3問で120分です。
2021年:110分
2020年:120分
2019年:150分
2018年:130分
2017年:110分
2016年:135分
2015年:125分
2014年:130分
2.合格ライン
第1問~第3問はキツイです。計算量だけで押し切れる第2問だけでもなんとか。
第4問、第5問は押さえないとこのセットではどうにもならない。第1~3問の難易度で焦っている中でとにかくやり切るしかない。
とにかく後半2問を取る。残り時間で第2問だけでもなんとか押し切れればOKでしょう。50%弱でも、今年は大丈夫なのでは。
3.各問の難易度
☆第1問 【2次関数+α】絶対値付き2次関数の最大・最小(C,40分、Lv.3)
2つの絶対値付き2次関数の和の最小値に関する問題です。見た目もそこまでややこしそうに見えませんし,最初の問題なので手を付け始めたものの、見かけよりずっときつくてあきらめた人がほとんどでしょう。東大で出そうな感じの問題。
(1)から手がつかない可能性もあります。要は、x≦0、1≧xではf(x)が右下がり、右上がりになることを示せばOKです。f(x)は連続な関数なので、これにより少なくともこの範囲での最小値はf(0)かf(1)です。
最小値の定義から任意の実数xでf(x)≧mですから、x<0でf(x)>f(0)≧m、1<xでf(x)>f(1)≧mが言えますね。
(2)が難しく、「最小値の候補」の考え方を用いないといけません。0≦x≦1においてもf(x)を場合分けして出していきます。直線と上に凸の放物線です。直線および上に凸の放物線において、最小値は端点でとります。したがって、場合分けの境目であるf(0),f(a),f(b),f(1)が候補です。
これらをすべて求めて大小を比較するのですが、この大小関係がa,bの値によって変化するので、さらに難易度が上がります。イメージとしては、0≦x≦a、b≦x≦1の範囲の直線(同じ式)が右上がりならf(0)が一番小さく、右下がりならf(1)が一番小さいです。
右上がりか右下がりかの境目はa+bが1以上か1以下かになります。あとは小さいと思ったものを残りの項から引いて0以上になるといいましょう。相当長い道のりで、グラフのイメージを答案としても大きな減点はないと思います。
(3)は(2)までたどり着けばなんとかなるのではないかと。最小値はa+b≦1ならab、a+b≧1なら(1-a)(1-b)です。和に関する条件から積の最大値を求めるなら、相加・相乗平均と相性がいいです。これが思いつけばほぼ一瞬で終わります。積≦和と使う形なので思いつきにくいタイプ。
思いつかない場合は、不等式条件での最大・最小なので領域図示でいきましょう(これは思いついてほしい)。例えばf(0)の場合、0≦a≦b≦1かつa+b≦1のとき、ab=kの最大値を求めます。双曲線を動かしてみて接するときです。f(1)のときも同様。どちらも、a=b=1/2のときに最大となります。
※KATSUYAの解答時間は26:17です。やること自体はムズくはないけど・・・って感じです。去年、9分しかかってないけど^^;
第1問についてはYouTube動画でも解説しておりますので、ぜひ参考にしてみてください。
第2問 【数列+ベクトル】ベクトルの成分計算、3項間漸化式(C、30分、Lv.3)
ベクトルの関係式から、Pnのx成分、y成分に関する漸化式を導き、一般項を求める問題。こちらも見た目より難しく、特に(3)は3項間漸化式に別の項が入るので、初見だと厳しいでしょう。第1問に引き続き厳しく、ここで追いつめられ始めた受験生も出てきたでしょう。配置がイジワル・・・^^:
(1)もなかなかうまく作れなかった人はいそうです。Pnに関してはOからの成分が与えられているので、OPnベクトルだろうがPnPn+1ベクトルだろうが、Oに始点を合わせればいけます。しかし、Qに関してはOに始点を合わせているだけだと成分が分かりませんので、逆にOQnが出てきたら、OQn+1も作って、引き算を作ることを意識しないといけません。
最初の条件について、そのままの式とn→n+1としたものを作りって辺々を引くとOPn、OPn+1、OPn+2と、あとQnQn+1だけが出ます。これで成分が全部分かるので、漸化式が作れますね。
(2)のxnは普通の3項間漸化式です。特性方程式を作って等比型の漸化式を2つ作り、辺々を引きましょう。なお、特性方程式の解の片方が1の場合は・・・みたいな方法はムダに覚えることを増やすだけです。重解の時以外はこの方法でOKです。
(3)は(1)で式が整理できていれば漸化式は簡単に立ちますが、ただの3項間ではなく{yn}以外の項が残ります。このパターンの問題は一度でも経験していないと厳しいでしょう。
この場合も、余計な項はなかったかのように振る舞います。特性方程式の解を使い、xnと全く同じ変形をします。今回なら、
y(n+2)-y(n+1)=a(y(n+1)-y(n))+a^(-n)
となります。普段はしっぽがないので等比数列になりますが、今回はここからさらにpa(n)+q^nの指数型の漸化式を解くということです。(本サイトでは6型と呼んでます) y(n+1)-y(n)=z(n)とでもおけば見やすいかと。
6型漸化式では、p^n+1かq^n+1で割って、階差型か4型(特性方程式c型)に帰着させます。個人的には後者がおすすめ。z(n)が出れば、階差から一般項に戻す公式でy(n)になります。
ベクトルの式変形もそこまで簡単ではなく、難しい3項間漸化式。文字も入っているため計算結果も繁雑で、こちらも正答率は低いと思われます。
※KATSUYAの解答時間21:20です。第1問、第2問両方キツイ。(3)は一般項にn=1,2を入れて検算したので多分大丈夫。これが続くとかなり苦しい。
第3問 【図形と式+微積分総合】(CD、50分、Lv.3)
領域図示の問題と、不等式の表す領域の面積の最小値についての問題。後半はそもそもどこが領域かもわかりにくく、かつ場合分けも発生し、面積の計算も多く、本セット最難問で、第1問、第2問よりもさらに難しいです。東大で出ても捨て問レベル。
第1問、第2問とあきらめて第3問ぐらいは・・・と思って取り組んだ受験生をさらに追い詰める難易度です。なぜこんな配置にしたのか^^;
(1)はyについて解けばOK。指数についているので、自然対数をとればいいでしょう。左辺≦中辺の方は微分して増減を調べて書きましょう。2つの領域がx=2,4で交わることがポイントになります。
(2)は捨て問です。まず、そもそも領域領域がどこをさしているのかを判別するのも一苦労。aの値によって2つの境界線の位置関係が変わります。しかもそれが、4通りもあるところが地獄レベルです。
因数分解型の領域は、1つおきに塗り絵するという考え方を使います。教科書通りの両方正か両方負ではあまりにメンドウです。4通りの場合分けが書けただけでも、試験としては勝ちでしょう。
しかし、メインはその面積。a≦elog2、6log(6)2≦aのときはそれぞれ減少、増加になることはさすがに、図形的に明らかとしてよいと思います。問題は残りの2つ。交点もキレイに出ませんので、その際はとりあえずα、βなどと置くしかないです。
そして、そもそも曲線側の領域にある関数の「x/logx」は(高校の範囲では)積分できません。(まずこれを知ってないと、この積分に考え込んでしまいます)
問題文は、最小となるαです。したがって、とりあえずS(a)を積分の式で表し、それを微分して増減さえわかればいいわけです。積分したものを微分ですから。例のもとに戻る系の微分だと分かりますね。ただしその際、交点もaが変われば変わりますので、交点もaの関数であることに注意。
2<a<6log(6)2のときでやっておきます。y=aとf(x)=log2・x/logx の交点をαとすると、グラフからα>4であることに注意。
こっちの方がまだラクという恐ろしい事実^^;
これらをもとに、f(x)の原始関数を考えることなく、微分を行うと増減が分かります。今回は、設定領域の2≦x≦6であることおよび、y=2と交わる点がx=2,4であり、この4が2≦x≦6のど真ん中であることによって、きれいに増減が分かれます。結果としてはa=2(x=2,4で交わる)のときが最小です。
aを動かしたときの面積の増減を考えると、なんとなくa=4のときであることは想像がつくと思います。サイアクそれだけ述べてa=2を導くのもあり。それでも、本問であれば上位10分の1ぐらいに入るでしょう。
※KATSUYAの解答時間は31:42です。さすがに3問連続で難しく、さらに本問は想定の範囲外で、自分の式変形が間違っているのかと思って最初からやり直したが、あっている。北大、本気出し過ぎ。東工大みたいな問題でキツイ。
第4問 【確率】円順列、隣り合う子音(B、20分、Lv.1)
HOKKAIDOの8文字を円形に並べる問題で、子音が隣り合うかどうかに関する問題です。条件付確率も絡んでいます。
前半の3問が嘘のような穏やかさで、問題を一通り見て、出来そうなものから手をつけるといういい教訓になりますね。(でも、ささすがに第1問からやりますよね^^;)。それでも、確率のことがきちんと分かっていないとこちらも間違えかねない問題です。
(1)は円順列でKやOなど、同じ文字を含んでいると難しく見えるかもですが、確率では同じものも区別するんでしたね(これを利用しないと本問も全滅でしょう)。すですので、8文字の円順列です。円順列では1つ固定ですので、Hを固定して7文字を並べます。HOKKAIDOの順に並ぶので、ほとんど場所は固定で、許されるのは同じ文字のOやKの入れ替えだけです。
(2)以降も、区別することに気づいていれば楽勝。存在する=少なくとも1つあると言い換えられます。少なくとも・・・と言われたら余事象です。子音が全く隣り合わない場合を考えましょう。隣り合わない場合は、間に入れていくことを考えましょう。
先に母音を並べておきます。AIOOなので1文字固定で3!。間の4か所に子音を入れるので4!です。全体から引くことを忘れずに。
(3)KKをカタマリにて同じことを行えばOK。4か所の隙間にH、D、KK(固めて)を入れるので、4P3です。KK内は入れ替え可能なので忘れずに。隣り合う→ひとくくりに固めておくことと、カタマリ内の並べ替えのセットです。条件付確率なので、この確率を(2)の確率で割りましょう。条件付確率の分母は「とき」の手前ですね。
※KATSUYAの解答時間10:40。急に簡単やな^^;前半に欲しい・・・
第5問 【微積分総合】zの軌跡、n乗の値(AB、15分、Lv.1)
最後は複素数平面からです。条件式を満たすzの軌跡を2つ出す問題と、n乗に関する問題。1つ1つは教科書レベルに近い問題で、前半の3問は何だったんだと言わんばかりの問題です。
(1)は、①が円、②が垂直二等分線でOKですね。
(2)共通解については、xとyの式に直して、図形と式の要領で交点を出す方が早い気がしますが、図形的にアプローチしてもいいと思います。zのまま数式で攻めるのはキツイです。直線の式があるときはx+yiと置いた方が見通しがいい事が多いです。
(3)は共通解が出れば楽勝。偏角だけに着目すればOK。負の実数なので、偏角はπの奇数倍となります。
※KATSUYAの解答時間は9:50です。難易度の差が激しすぎないか・・・逆に拍子抜け。
4.対策
頻出分野は数IIIからは微積と複素数平面(久しぶりに出題)、あとは整数、確率、図形で、数Bはどちらか1問でると思われます。(今年は第2問に数列+ベクトル融合で出ました)
今年はケタ外れに難しいですが、北大は旧7帝大の中ではかなり標準的かつ良問の組み合わせになっており、過去問自体が入試演習に最適です。もちろん、その前に原則習得はしっかり終わらせておきましょう。その後、入試基礎演習、入試標準演習の代わりに、過去問を用いてもいいと思います。
今年の難易度が続くのかどうか・・・なんとも言えませんが、受験生全体の出来次第だと思います。
また、東大や京大などの最難関を受験する人たちは受験初期に15年分ぐらい一気に演習してみてもいいでしょう。
量をこなす演習:じっくり演習=7:3ぐらいでしょう。
以上です^^
■他年度の、本大学の入試数学■
>> 2010年度
>> 2011年度
>> 2012年度
>> 2013年度
>> 2014年度
>> 2015年度
>> 2016年度
>> 2017年度
>> 2018年度
>> 2019年度
>> 2020年度
>> 2021年度
■関連する拙著『Principle Piece』シリーズ■(大幅にリニューアルしました!!)
★ 数学I 2次関数 (第1問)
★ 数学A 集合と場合の数 (第4問)
★ 数学A 確率 (第4問)
★お知らせ★
過去にTOP10を独占した数学の問題集『Principle Piece』シリーズの販売再開!
こちらも、原則習得のための参考書です。
YouTube開設しました。 個人的に紹介したい大学入試数学を中心に解法や発想を動画にしてみようと思います。
Twitter始めました こちらもよろしくお願いいたします^^