慶應大学医学部数学講評| 2024年大学入試数学

2024/02/21

※動画、画像が読み込まれないときがあります。その場合、画像なら余白を、動画は文字リンクをクリックしてください。

●２０２４年度大学入試数学評価を書いていきます。今回慶応大学(医学部)です。

２０２４年大学入試（私大）シリーズ。
慶応大学(医学部)です。

問題の難易度（易A←→E難）と一緒に、典型パターンのレベルを３段階（基本Lv.１←→高度Lv.３）で書いておきます。
また☆は、「解くとしたらこれがいい」というオススメ問題です。

また、解答までの目標時間を、問題ごとに書きます。
※目標時間＝解き方を含め、きちんと完答するまでの標準的な時間です。

したがって、目標時間を全部足すと、試験の制限時間を越えることも、当然ありえます。
同時に、その時間の２倍考えてもまったく手がつかない場合は、ヒントや答えをみるといい、という目安にしてください。

★お知らせ★

Principle Pieceシリーズの販売中です＾＾　原則習得のための参考書です。

YouTubeチャンネルです　個人的に紹介したい大学入試数学を中心に解法や発想を紹介していこうと思います。

Twitter　こちらもよろしくお願いいたします＾＾

慶応大学（医学部）
（試験時間100分、4問、ハイブリッド型）

１．全体総評～昨年よりは難しいが、例年比では易しめ～

調査以来もっとも易しかったと思われる昨年よりはさすがに難しいですが、それでも反動というほどではなく、例年に比べれば易しい方です。もちろん、

どの大問も前半は比較的取り組みやすいものが多いので、穴埋めを利用して計算をしつつ、うまく捨てれば結構稼ぎやすいセットだったと思います。

試験時間100分に対し、
標準回答時間は152分【97分】（←穴埋め考慮）2年連続、ギリギリ制限時間内です。空間の後半を捨てればもっと短い。

2023年は133分【91分】

2022年は169分【111分】

2021年は203分【123分】

2020年：177分【113分】

2019年：164分【106分】

2018年：197分【124分】

2017年：185分【128分】

2016年：200分【125分】　

2015年：213分【115分】

2014年：165分

※本エントリーの【　】内は、慶応医学部受験者層のレベルを考慮していますので、その他の大学に比べて短めです。それでも、100分をオーバーすることがほとんどです＾＾；

２．合格ライン(科目全体では60％)

第１問の穴埋めは今年は10個。今年も易しめでしたので、慶應医なら出来れば全部欲しいところ。

第２問のは慶應医お得意の確率と漸化式ですが、誘導が丁寧すぎるので難易度は下がり気味。これも慶應医なら全部取れるはず。サイアクでも「さ」までは欲しい。

第３問も最後の「こ」を除けば方針も迷うことはなく、カリカリ計算するだけなので取れるはず。(4)は計算が繁雑なので飛ばしてもいいかも。

第４問は本セット最難問。立体の感覚がないと（３）以降はかなりキツイと思われる。ここにどれだけ時間をさけるかだが、無理なら他を見直して正答率を限りなく上げたい。

今年はキー問題というキー問題はないかも。簡単なところを計算ミスせず。70％ぐらいは欲しいかもしれませんね。

３．各問の難易度

第１問（１）【図形と方程式】三角形の外心と内心の座標（B,13分【7分】、Lv.２）

座標で当たられた3点を頂点とする三角形の外心と内心を求める問題。慶應医ならただの計算問題でしょう。

外心は教科書レベルですね。3点を通る円の中心です。x=3/2上にあることを利用し、さらに原点を通ることまで利用すると、ｙの1次の係数だけ設定して円の式x^2-3x+y^2-2by=0のように書けます。あとはBを通ることを式にすればOK。

内心は教科書レベルではないですが、角の二等分線の交点として求められます。しかも∠Oの二等分線が簡単に分かるので、あと1本出せばOK。∠Aの二等分線がやりやすいですね。角の二等分線は２つ出ますが、図をかけば、傾きから明らかにどちらかは分かりますので、それを利用しましょう。

Principle Piece

内心の位置→角の二等分線の交点＋図で候補を絞る

（詳細は拙著シリーズ数学II 図形と方程式 p.86 参照）

知識がある場合は以下のように２通りの方法で短縮できます。

OからOA上の接点までの距離が(OA+OB-AB)/2で出せることを知っていると、これがｘ座標、∠Oの二等分線上だから、その1/√3倍がy座標として出すことも可能です。

内心の位置ベクトルの一般式を知っている場合は、OAベクトルとOBベクトルに対し、(２OA+3OB)／(2+3+√7)となります。有理化の作業があるので、３辺の長さが無理数ばかりのときは避けた方がいいかもです。

※KATSUYAの解答時間は3:12です。内心は接点までの距離を利用して知識で出しました。穴埋めはベンリですねぇ。

☆第１問（２）【式と曲線】楕円と接線、面積（A,14分【8分】、Lv.1）

微積分総合と聞くとムズそうですが、接線の式と面積を求めるだけです。拙著にもほぼ同じ問題あります＾＾

最初は接線の傾きを聞いています。接線の公式にあてはめるだけですね。

後半は面積ですが、最初の誘導がいやらしく、この手の問題は媒介変数の方がラクです。

Principle Piece

楕円絡みの問題 → 媒介変数表示が有効

（詳細は拙著シリーズ数学B・C 式と曲線 p.38 参照）

媒介変数表示で置けば、簡単に分母がsin２θだけになり、これが１になるときに最小だと分かります。

※KATSUYAの解答時間は計3:03です。なんで最初に(X,Y)で置いて傾き出させるんや＾＾；ってことで誘導無視で媒介変数で置いて終了。

第１問（３）【微積分総合？】三角関数の最大値、面積（A,10分【6分】、Lv.1）

今年もここに微積分総合っぽい問題ですが、最大値は数Ⅱの微分で行けるし、面積も積分計算が簡単です。落とせません。慶應医でなくても落とせません。

前半はそのまま微分してもいいし、倍角でθにしたあとにcosをsinに変えれば、sinの３次式になりますので、数Ⅱの微分でもいけます。

後半は面積なのでそのまま積分しますが、倍角で2cos^2θsinθにすれば、第２置換がすぐに見えます。

Principle Piece

(sinの式)cos、(cosの式)sin は第２置換積分

（詳細は拙著シリーズ数学III 積分法(数式編) p.19 参照）

※KATSUYAの解答時間は計1:34です。KO医って最近、大問１簡単になったな・・・

☆第２問【確率＋数列】確率と漸化式（Ｂ、25分【16分】、Lv.2）

今年もいつも通り2番は確率で、慶應医の１８番である確率と漸化式が帰ってきました。しかし誘導過多のため、慶應医であればあまり差がつかないぐらい難易度が下がっています。穴埋めの数かせぐにはこうやって出すしかないんですかね。

確率と漸化式の基本３原則はこちらになります。今年だけで何回書いたか＾＾；

Principle Piece

[1]n回目からn+1回目の遷移を詳しく [2] 必要のない部分も文字で

[3] 確率の和が１、対称性も活かす

（詳細は拙著シリーズ数学B・C 数列 p.78 参照）

今回は(1)で原則[1]が、(2)で原則[2]ががっつり示されています。これらは、誘導が無くても自分で置けるようになっておきましょう。

ａｎとｃｎが状況的に対称であることからも、bnの漸化式を見るとanとcnの係数が等しいです。係数が等しいものはラッキーですね。原則[3]によって１－ｂｎに出来ます。

出来たｂｎの漸化式は４型ですから、簡単に出せます。

最後は聞き方がちょっと意地悪。この誘導だと、anの漸化式にbnの答えを代入して、指数型の漸化式に帰着させることになります。もちろん、それでも解けます。今回のような場合は、汎用性の高い階差型に帰着させた方がいいです。

Principle Piece

漸化式６：指数型は[1]４型　か [2] 階差型　に帰着。n+1乗で割る

（詳細は拙著シリーズ数学B・C 数列 p.40 参照書籍では式も含めてちゃんと書いてあります）

しかし、今回は、初期状態がＢであることと対称性を考えると、an=cnですよね。従って、an=(1-bn)÷２です。その答えに2^nをかけたものがdnですね。こっちの方が早いです。

※KATSUYAの解答時間11:46。漸化式戻ってきたけど、おもてなし精神強すぎませんかね？これはあまり差がつかなさそう。結局去年よりかかってない。

☆第３問【微積分総合+極限】極値、グラフの概形、共有点条件、面積計算、極限（BC、30分【20分】、Lv.2）

今年も微積分総合＋極限という感じです。題材は全然違いますが、難易度は昨年と同じぐらい。昨年より少し計算量は少ない気がしますが、最後はメンドウで、捨てるのが正解だったかもです。

(１)(２)は微分するだけです。

(２)って記述ですかね。概形書くだけなら、f'(x)の符号を見て、ささっと書いてしまえばOKです。記述なら、増減表や漸近線付近の極限を調べる必要があります。定義されないｘが多いので、まあまあメンドウ。対称性を活かしてｘ＞０だけ調べると記述量は減ります。

(３)は(２)のグラフから、第２、第４象限で２点ずつ交わることになると分かります。原点を通る接線を求めることに帰着されるので、まず接点をおき、それが原点を通るとすればいいでしょう。

ULTIMATE Principle Piece

曲線外から引いた接線はまず自分で接点をおく

（詳細は拙著シリーズ数学II 微分法 p.15 参照）

(４)はただの部分分数分解です。まずx(ｘ－１)とx(ｘ＋１)に分け、それぞれをまた部分分数分解するとほぼ暗算に近い形で可能です。

(５)はA(m)ですが、交点が汚いのでとりあえずx(m)で計算し、積分計算をしきったらx(m)を求めて直すという方法が良かったと思います。x(m)は一見出なさそうに見えますが、分母を払えばx^2の２次方程式とみなせますね。答えの式もx(m)の２乗ばかりなので、うまく設定していると思います。でも計算はまあまあメンドウ。

最後の極限はmのままだとかなり見えにくく、詰まった人が多いと思います。x(m)のままの方が全然見やすいです。ｍ→+0のときにx(m)→∞になります。あとは、logと整式絡みなので、eの定義式に持ち込む原則を意識していればすんなり見えたと思います。

Principle Piece

指数・対数型の極限 → 基本系４つに帰着させることを意識する

（基本系４つの詳細は拙著シリーズ数学III 微分法１ p.47 参照）

x(m)のままでも見づらいですが、私はx(m)-1の逆数をNとし、N→０としたときの極限にしました。そうすればlog(１＋N)/Nに出来ます。ちょっと慣れてないと難しい変換かもしれません。対数と多項式を必ず分母と分子に置きたいので、多項式の方(logの無い方)をムリヤリ分母に置きたい、という着想による置き換えです。

※KATSUYAの感想：解答時間16:14。「く」まではサクサク。「け」からメンドウに。最後は結構迷ったけど、とりあえず上の着想でムリヤリ多項式側を分母にしてみたら基本系に出来たので安心。なお、行けた！って調子乗ったのか、 logはいっているのに、普通に「ｅ」って答え書いてました＾＾；何しとんじゃ。

第４問【空間ベクトル】四面体の切り口と面積、体積、六面体の面構成、切り口（CD、60分【40分】、Lv.3）

最後は空間ベクトルから。それまでが穏やかだったからか、最後の後半はかなりキツイです。数式でごり押すのもかなりキツく、ある程度空間上にちゃんと描く必要がありますが、それでも見えにくい。難問です。

(1)から点の設定の仕方がいやらしい。最初にどれがどれか考えると迷います。4面体は6辺あり、うちＢＣとＯＡは１＜ｚ＜２を含まないはずなので、残り4辺との交点のはずです。なので、辺上の点を１－ｓ、ｓの係数設定でもして表しつつ、ｚ座標がｔとなるようにｓを決めて、先に全部の座標を出すといいでしょう。

それで、ｔ＝１としたときにＡとかぶるもの、ｔ＝２としたときにＢとかぶるものを見て、Ｗ，Ｘ，Ｙが判断できます。Ｗは両方に近づくので、それで全部決まります。

あとは4点のｘ、ｙ座標だけ見て慎重にｚ＝ｔ上にプロットするだけです。１＜ｔ＜２であることに注意すれば、大小関係が決まるものが殆どですので、位置関係もある程度分かるでしょう。

面積を出すときに、底辺や高さに（２－ｔ）や（ｔ－１）などが出てくることも安心材料です。１＜ｔ＜２で確かに正になる値ですからね。こういうところでの確認も、検算の１種です。

なお、体積はＡ(ｔ)を１~２まで積分し、あとは上端と下端の三角錐を足します。上は底面積A(2)、高さ１、下は底面積Ａ(1)、高さ１としてＯＫですが、穴埋めなので、4点座標型の公式を知っていればそっちが早かったかもしれません。慶應医なら知っておきたい準公式で、私も間違いなく慶應医受験生なら覚えておくように言います。

（拙著シリーズ数学Ｂ・Ｃ空間ベクトル p.78より抜粋）

これを用いると、簡単に「こ」は求めることが出来ます。

（３）は以降は難しい。点Ｄが追加されますが、これがまた結構微妙な位置にあり、ある程度座標を意識して書いてもなかなか判定が難しいです。最初は穴埋めを存分に生かします。構成面を見ると、Ｏが全部入っています。もしこれでＡＢＣが入ると、それで四面体になるので、ＡＢＣは入らないはずです。なので、ＡＢＣが表面に出ないように3面取るには、Ｏを全部Ｄに変えてあと3面とるしかないですね。

これ、3面与えられてなかったからかなりキツイと思います。というか、取り方によるのでは？と思います(OBCを表面に出さないような6点でも取れる)。

次の「せ」「そ」は面が分からなくても行けます。平面ＡＢＣの点とＯＤとの交点は直線に始点が入っているので、こちらの原則ですね。

Principle Piece

交点１：平面は1-s-t,s,tの係数、直線は実数倍設定

（拙著シリーズ数学B・C 空間ベクトル p.33 参照）

最後の切り口ですが、Dが加わったので、DO~DCまでの交点の考察が必要。1<z<2にないDB,DCはムシ、DOとの交点は場所からしてOBCの外側なので切り口にならず、残りDAとの交点だけ追加して面積を出しますが、図形的な位置関係がうまく把握できていないとかなり厳しいと思います(特にODとの交点が入るかどうか)ので、捨ててもいいでしょう。

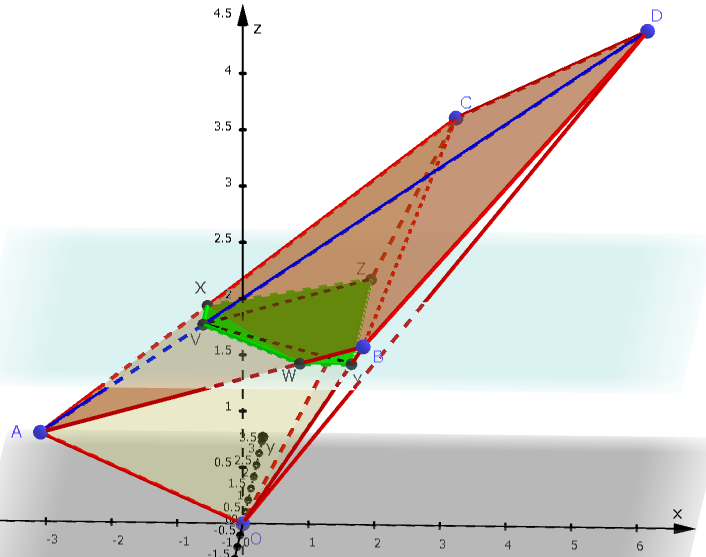
なお、切り口はこんな感じになります。頂点の名前は、ADとｚ＝ｔとの交点をVと置いています。

コンピュータに書かせてアングルいろいろかえてもかなり見にくい図です。手書きで書けるわけがない＾＾；

※KATSUYAの解答時間は32:42です。(1)からまあまあメンドウ。(2)は積分させたいんやろうけど、外積でさっさと処理。(3)からキツイ。ABCが中に来るようにしたいからということで判断。図をいったん丁寧書き直してみるも、イマイチ分からず。相当辺な立体では？とりあえず交点Eは原則に従って出す。最後切り口。また交点出すの？きつすぎ。でもDAとDOだけか。これ加えて足せばいいのかな。でも最大値ない形になるけど。どっちか入らない？もう一回図を書き直す（９×３×４の直方体を意識してOABCDを取るぐらいの気持ちで）。面OBDとか面OCDは表面じゃないからODとの交点の方は入らないのか。これ相当キツイと思う。本番なら最後２つは即捨てだわ。

４．対策～癖と計算力の多さに慣れる～

傾向、形式ともに癖の強いセットです。ここ最近は出てませんが、確率と漸化式は名物で、微積と極限もボリュームの大きいものが出ます。計算力、演習ともに必要です。
高校２年生の段階でも、典型パターンの7割が習得済みであることが望ましいです。共通テストですでに７，８割とれるようなレベルにいないと厳しいでしょう。本学受験生の高２で、数IIIにまだ手がついていない人は、いますぐ独習してください。そんなペースでは本学部の試験には耐えれません。

高３に入ったときには原則習得段階は終えて、入試問題演習に入りたいところです。夏以降はさらにレベル高めの入試演習、を行い、仕上げ段階まで行ってから過去問、といった感じでしょう。理工学部もレベルや出題内容(確率と漸化式はかなり似ています)、形式が似ているので、使えます。

量をこなす演習：じっくり演習＝６：４ぐらいでしょう。３年生になったらできる限りじっくり演習したいです。2時間でも考え込んでしまってもOKです。

ただし、あらゆる手段（明らかに計算すると途方もなく時間がかかりそうでも、それで押し通してみる！）で手を動かしてみることです。答えにたどり着かなくても、計算力は着実にUPしていきます。普段の練習から「これ計算するん？無理やろ～」と思ってあきらめるのはNGです。そんな計算は慶應医であれば平気で出ます。

以上です＾＾