東北大学理系数学講評 | 2024年大学入試数学

2024/03/05

※動画、画像が読み込まれないときがあります。その場合、画像なら余白を、動画は文字リンクをクリックしてください。

●２０２４年度大学入試数学評価を書いていきます。今回は東北大学(理系)です。

いつもご覧いただきまして、ありがとうございます。　KATSUYAです＾＾いよいよ、２次試験シーズンがやってきました。すでにお馴染みになってきたかもしれませんが、やっていきます。
２０２４年　大学入試数学の評価を書いていきます。

２０２４年大学入試シリーズ（国公立）シリーズ。
東北大学(理系)です。

問題の難易度（易A←→E難）と一緒に、典型パターンのレベルを３段階（基本Lv.１←→高度Lv.３）で書いておきます。
また☆は、「解くとしたらこれがいい」というオススメ問題です。

また、解答までの目標時間を、問題ごとに書きます。
※目標時間＝解き方を含め、きちんと完答するまでの標準的な時間です。

したがって、目標時間を全部足すと、試験の制限時間を越えることも、当然ありえます。

同時に、その時間の２倍考えてもまったく手がつかない場合は、ヒントや答えをみるといい、という目安にしてください。

★お知らせ★

Principle Pieceシリーズの販売を再開しました＾＾　原則習得のための参考書です。

YouTube開設しました。　個人的に紹介したい大学入試数学を中心に解法や発想を動画にしてみようと思います。

X(旧Twitter)です　こちらもよろしくお願いいたします＾＾

東北大学（理系）
（試験時間150分、６問、記述式）

１．全体総評～後半を中心にかなりきつく難化～

難化です。昨年は6番以外は例年以下の難易度で点数に結びつきやすかったですが、今年は全体的にレベルが底上げされ、特に広範な難易度が高いく、難易度の差に受験生はとまどったかもです。これまでにもこのレベルのセットだったことはありますが、ここ最近ではかなり難しいですね。

数III絡みは普段は後半2題に来ることが多いですが、今年は第3問も加わり３題です。残りは数Ⅱの微積、数列、ベクトルです。難関大以上でよくみられるの確率＋BIII出題ですね(Bにベクトル含む)。

試験時間150分に対し、標準回答時間は175分。ここ最近では重めです。

2023年：158分

2022年：168分

2021年：155分

2020年：125分

2019年：190分

2018年：185分

2017年：170分

2016年：135分

2015年：178分

2014年：185分

2013年：155分

2012年：170分

2011年：140分

2010年：200分

２．合格ライン

第１問は文理共通の問題。カリカリ計算するだけなのでおさえたい。全体のセットを考えても完答必須。

第２問も文理共通。理系ならサイアク微分すればいいので、これも出来てほしい。

第３問は確率と漸化式。設定、誘導は丁寧なので(3)まではなんとか正解したい。(4)はキー問題か。

第４問は空間ベクトルで本セット最難問(同率１位)。経験がないと(3)から(4)につなげにくい。(2)どまりが多いか。(3)まで出来れば有利。

第５問もキー問題。類題は見たことがあると思いますが、うまくアレンジして難易度を上げています。

第６問は第４問と並んで最難問。曲面の一部の面積を求める問題でこちらも難しい。(1)どまりの人も多いか。サイアク(2)を使って(3)を解くという手もあり。

第1,2問をおさえ、第３問と第4問を途中までかじる。第3問が最後まで行けて、第5問が押さえられればかなり強いので、第5問が合否を分けそう。55％強ぐらいか。難しいとはいえ、小問のおかげで白紙にはならないハズで、ある程度の点数はかき集められる。

３．各問の難易度

第１問【微積分(数Ⅱ)】放物線と接線、面積（B,20分、Lv.2）

数Ⅱの微積分に関する問題。放物線の一部と2直線で囲まれた部分の面積を求めます。文理共通問題で、どちらでも落とせないです。

(1)は直線OAは頂点を出せば出せますので、もう一回放物線と連立すればOK。接線はこちらの原則。

ULTIMATE Principle Piece

曲線外から引いた接線はまず接点をおく

（詳細は拙著シリーズ数学II 微分法 p.15 参照）

接線の式が原点を通るとして求めます。傾きが正の方です。ｐ＞ｑは両方出せばすぐにわかります。

(2)は領域を図示すればＯＫ。0～2aまでは直線の間、2a～4aは直線と放物線の間です。

(3)は(２)が出ればおまけみたいなもんですね。

※KATSUYAの解答時間は10:23です。最初は普通の問題でサクッと終了。

☆第２問【対数】不等式の証明、対数不等式の整数解（B、20分、Lv.２）

不等式の証明と、それを利用して対数不等式の整数解を求める問題。(１)をうまく(２)につなげることが出来ればそんなに難しくはないです。理系なら正解したい。

（１）はまず、(ｂ)から直ちにx+1≧2log_t x+1 が言えますので、あとはそれが2log t(x+1) より大きいと言えればＯＫ。

真数部分はtx^2と(x+1)^2となりますが、(ａ)の条件がキレイに使えて、tx^2の方が大きいと分かりますね。

(２)はまともに解くのはムリです。「違う種類の関数が混じっている方程式を、数式の変形で解いていくのは基本的にはムリ」と思っておきましょう。そうすると、（１）によって範囲を絞るという発想にいたります。

また、左辺と右辺は、明らかに左辺の方が大きくなっていきます(理系ならこの感覚はあるはず)。従って、ある程度のところまで調べて、右辺が小さくなり出したら、(１)が使えるのではないかと考えるわけです。

ｎ＝４で等号が成り立ちます。(１)に戻ってみましょう。ｔ＝２、ｘ＝４とすると(a)(b)の条件をともに満たすので、帰納的にn=5以降はすべて左辺の方が大きいことになります。従って、ｎ＝１，２，３，４だけで考えればいいことになりますね。

サイアク思いつかなくても、理系であれば例えば真数比較で行くと2^ｎ≦n^2 となります。よく見る形で、2n乗根とって対数取ればlog x/xに帰着出来るタイプですね。(なお、５番もこのネタのアレンジ)

※KATSUYAの解答時間は8:24です。理系ならｎはあんまり大きくないってすぐ分かるはずやからそんなに難しくないかな。

第３問【確率＋数列＋複素数平面】確率と漸化式、確率が等しくなる条件（Ｃ、30分、Lv.2）

旧７帝大が大好きな確率と漸化式からです。今年は東大、東工大、東北大が出しました。だいたい２つか３つぐらいが出す感じです。本問は設定もすべて問題文に書かれており、遷移を見ること、処理の誘導も(1)～(3)にありますので、そんなに難しくないです。(3)は差がついたかも。

まずは確率と漸化式の原則３点セットの確認をしましょう。

Principle Piece

確率と漸化式原則３点セット

[1]n回目からn+1回目の遷移を　[2]必要のない部分も文字で

[3]確率の和＝１、対称性も活用せよ

（詳細は拙著シリーズ数学B・Ｃ数列 p.78 参照）

今回は問題文にすべて文字で置かれています([2]の原則)。これに従って、慎重に遷移図を書けば(1)はクリア。

(2)も(1)が出来れば、その漸化式を立てるだけ。うまく等比型になります。

(3)も基本的には(1)と同様。ちょっと係数調整がメンドウですが、同じ係数が出てくるはずなので、p_nの係数でくくってみましょう。

(4)は(2)と(３)を使います。p(n)とr(n)を聞かれていますので、(3)の２式からqnを消去するという発想になったかどうかですね。

そうすると虚部にうまくp(n)－r(n)が出ます。よって、虚部がゼロになればOKということです。あとはドモアブルで終わりですね。

※KATSUYAの解答時間は16:35です。(4)は少し迷った。(２)で式１つ、(３)で実部と虚部の２式２つで、p,q,rは全部出るはずなので、全部出すつもりでまずqnを消去したらうまく出てきたのでいけた。(４)は出来れば有利かな。

☆第４問【空間ベクトル】２つの球面の交線(円)上の点とxy平面との距離（CD、40分、Lv.３）

空間ベクトルからで、２つの球面の交わりである円について考察します。経験があれば流れは見えるのですが、初見では何をしたくて(3)があるのかが見えない。レベル高めのパターン問題なので、本セット最難問の１つでしょう。

(1)はいいでしょう。これだけめっちゃ簡単＾＾；

(2)の証明は、２円の関係とほぼ同じ。中心間の距離と半径の和、差に関する関係ですね。半径は求め方は様々かも。S1とS2の交線を含む平面Hは、２円の交点を通る直線の要領で、辺々を引くと出せます。

あとは、S1の中心と平面の距離を求めれば、３次元バージョンのこちらの原則が使えます。

Principle Piece

球面の平面による切り口 → dとrと三平方で

（詳細は拙著シリーズ数学B・C 空間ベクトル p.46 参照）

ｄが出ることで、(１)と合わせれば、P3は２：１に内分する点だと分かりますので、P3も出せます。S1から平面Hへの垂線の足として出してもOK。

(3)は(4)のための準備になりますが、初見だと何をしているのかよく分からないと思います。拙著『Principle Piece 数学B・C～空間ベクトル～』だとめっちゃ詳しく載っていますので、お持ちの方はp.66～ｐ.70をご覧ください。

ここでは、ざっくり流れをいいます。斜め平面上にある円を扱う際の原則です。

Principle Piece

斜め平面上の円周上の点 → 自分で垂直なベクトルを２つ見つける

（詳細は拙著シリーズ数学B・C 空間ベクトル p. 参照）

単位円でいう、(1,0)と(0,1)のようなものを見つけたいってことです。そうすれば、cosθ倍とsinθ倍の結合で表せるからです。

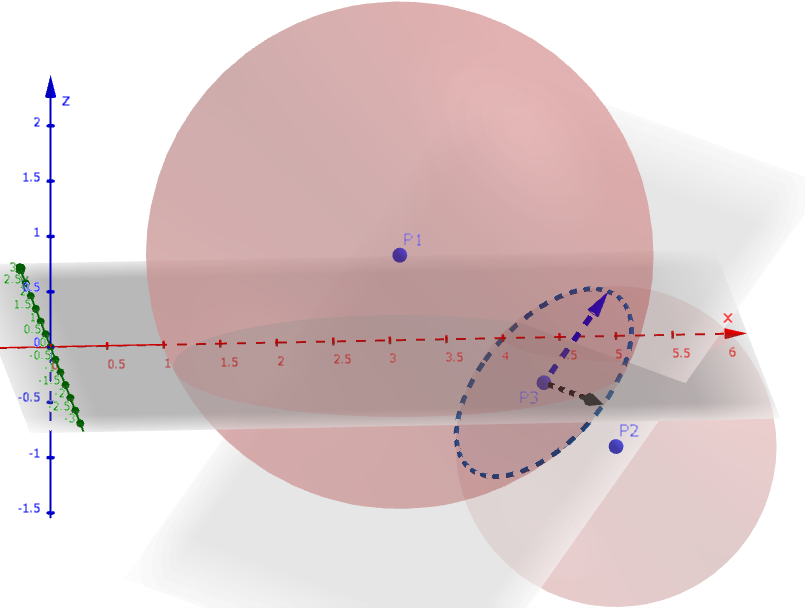
下図の黒のベクトルと青のベクトルです。

そのうちの１つ、黒の方(とその反対向き)が(3)のベクトルです。xy平面に平行にする理由は、求めたいのがｚ座標の範囲(xy平面との距離なので、大事なのはz座標の絶対値)だからです。２ベクトルのうち１つが、ｚ座標がゼロになるものであればラクですよね。

すなわち、(x、y、０)でかつ平面Hに入っているものです。すなわち、P1P3ベクトルと垂直なものです。これで出せます。操作的には、x成分とy成分を入れ替えて、片方符号変えればOKです。

もう１つは、やはりP1P3に垂直で、しかも(３)にも垂直なベクトルを見つけます。あとは長さ１への調整をしてください。

これにより、ナナメ円上の点はOP3ベクトル＋２つのベクトルのcosθ倍、sinθ倍になります。片方はz成分をゼロにしているおかげで、ｚの範囲はすぐにわかりますね。

もし(３)の誘導が無ければ、こちらの方法でもできます。答えだすだけなら、こっちの方が速いです。

Principle Piece

斜め平面上の円の座標範囲 → 連立方程式の実数解条件

（詳細は拙著シリーズ数学B・C 空間ベクトル p.67 参照）

平面Hの方程式はS1とS2の式を引けば出ます。そこから１文字消去(zは残す)し、S1かS2に代入します。すると２文字になります。zを係数とみなし、残りの文字についての２次方程式になりますので、実数解条件でｚを出すことが出来ます。

※ＫＡＴＳＵＹＡの解答時間24:38です。これ、(3)だけで(4)出させるのは多分類題経験がないとムリやと思う。てか、(3)なければ普通に実数解条件で済ますけど＾＾；　一応問題の誘導に従って出すか。こっちの方が時間かかるんよなぁ。まあ図形的な意味も理解できるし、演習問題としてはありやねんけど。入試としてはいやですね。

第５問【微分法の応用】導関数とグラフ、方程式の解（BC、30分、Lv.2）

数Ⅲの微分法からです。よく見かける、m^n=n^mの自然数解のアレンジバージョン。適度に難易度が挙げられており、良問だと思います。差もつくでしょう。

（１）微分して形に合わせるだけ。

（２）は問題文通りですが、（１）からの流れをおさえましょう。分子だけを取り上げて様子をつかむというのはよく用いる手法です。

Principle Piece

f(x)/g(x) 型の導関数は分子だけに着目して様子をつかむ

（詳細は拙著シリーズ数学III 微分法２ p.57 参照）

分子だけをもう一度微分し、単調減少分かったら、中間値の定理との合わせ技ですね。適当な値を代入して負になることを示します。大きい値を入れれば余裕ですが、(4)を考えると、出来る限り小さい値を入れた方がいいと思います。このあたりがちょっと難しいところ。

(3)は(2)と、問題文に与えられた極限も利用すれば増減表もグラフも書けます。

(4)はm^n=n^mのアレンジ版。対数とって、mnで割るとf(x)の形になります。(2)でαの値をある程度絞っていると、ｍの候補は少なくて済みます。うまく調べると、ｍ＝３，４のときだけで済みます。

m=3のときはn=6となることが分かります。グラフから6が見つかればOK。m=4のときも、グラフからあるとすればn=5のみですが、不適だと分かりますね。

※ＫＡＴＳＵＹＡの解答時間は20:00ちょうど。(4)を見て、(2)で範囲を狭めなおしました。有名パターンのアレンジで、適度にメンドウになってるので、これはちょうどいいかな。

☆第６問【微積分総合】円錐の側面の一部の面積（C、35分、Lv.３）

最後は積分法(グラフ)からで、円錐の側面のうち、ｚ＝ｘで切られた部分の片側の面積を求める問題です。(2)がコアになりますが、サイアク(2)を受け入れれば(3)は積分計算可能です。

(1)は交点を求めるだけです。PQ上にあるので1文字で表し、かつｚ＝ｘ上にもあることでｔを求めます。あとはPQの実数倍として求めればOK。

(2)はなかなか難しいかもしれません。まず側面の話なので、展開図を考えるのはいいと思います。最短距離の問題でよく見る原則ですね。

Principle Piece

側面での最短距離は展開図で

（詳細は拙著シリーズ数学I 三角比 p.66 参照）

次に、証明すべき不等式を見ます。両辺の形から、おうぎ形に近似することを思いつきたい。(1)から、鋭角の範囲ではθについて単調増加ですから、半径がr(θ)のおうぎ形と半径がr(θ+h)のおうぎ形の間です。

あとは中心角です。答えの形からも予想したいですが、中心角θの1/√2 倍のはずです。1/√2倍がどこから出てくるかが分かればこちらの勝ちです。θは底面上の円での角度です。底円上で角度がｈだけ動くと、弧上ははｈ動きます。側面の弧で同じだけ動くためには、中心角が1/√2倍になりますね。(T進さんの解答だと分かりやすい図があったと思います)。

(3)は(2)から、θが0以上の範囲でのS'(θ)が求められます。これと(1)の結果から、S(θ)は積分で出すことが出来ますね。積分は問題文にもある置換を利用しましょう。誘導が無いことはほとんどないですが、三角関数の分数式の積分は、この置換が有効であることを、余裕があれば覚えておきましょう。

Principle Piece

三角関数の分数式の積分 → 奥の手は tanx/2=t の置換

（詳細は拙著シリーズ数学III 積分法(数式編) p.81 参照）

※ＫＡＴＳＵＹＡの解答時間は23:18。題材的には去年よりハイレベルやけど、知識があると今年の方がマシ。多分今年のこの問題の方が平均得点率は低いかな。(2)は証明なので丁寧めに記述。

４．対策

たまに非常に難しいセットになることが多いです。と毎年書いてますが、今年はそれに該当しますね。例年は標準レベルの問題が出題されます。難しい年に対応出来ればそれが一番いいですが、他の科目とのバランスを考えると、あまり振り回されるのも考えものです。2021年、2022年、2023年あたりの難易度が例年並みでしょう。(エントリーの上にある制限時間基準で見てます)

ひとひねり加えられたり、融合的なものが多いですが、やることは典型的なものが多いです。

頻出分野は微積分、確率、整数問題(今年は出ず)、図形です。さらに複素数平面が３年連像出題。計算量が多いものも出ますので、素早く確実に解けるようにしましょう。

パターン問題を習得したあと、入試問題の表現に数多く触れることが大事ですね。最終段階は入試標準レベルでも大丈夫ですが、不安な場合は仕上げ段階まで行いましょう。

なお、拙著『Principle Piece』シリーズであれば「原則習得」「入試基礎演習」の両方の段階を兼ねていますので、この後にもう入試標準演習の問題集に接続可能です＾＾

量をこなす演習：じっくり演習＝７：３ぐらいでしょう。

以上です＾＾

東北大は単科長年タイプのものもありますので、過去問対策はこちらでもいいでしょう。